题目内容
指出函数y=ax3+1的单调性,并加以证明.(其中a是非零常数)
分析:当a>0时,设<x1<x2 ,计算 f(x1)-f(x2)=a(x1-x2)[(x1+
x2)2+
]<0,可得f(x1)-f(x2)<0,从而y=ax3+1是增函数.当a<0时,同理可证,y=ax3+1是减函数.
| 1 |
| 2 |
| 3 |
| 4 |
| x | 2 2 |
解答:解:当a>0时,设-∞<x1<x2<+∞,y=f(x)=ax3+1,则f(x1)-f(x2)=a(x1-x2)[(x1+
x2)2+
].(10分)
由题设可得 x1-x2<0,由于(x1+
x2)2与
不可能同时为零,[(x1+
x2)2+
]>0,
所以f(x1)-f(x2)<0,从而y=ax3+1是增函数.(12分),
当a<0时,同理可证,y=ax3+1是减函数.(14分)
| 1 |
| 2 |
| 3 |
| 4 |
| x | 2 2 |
由题设可得 x1-x2<0,由于(x1+
| 1 |
| 2 |
| 3 |
| 4 |
| x | 2 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| x | 2 2 |
所以f(x1)-f(x2)<0,从而y=ax3+1是增函数.(12分),
当a<0时,同理可证,y=ax3+1是减函数.(14分)
点评:本题主要考查函数的单调性的判断和证明,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ;②y=x2-3|x|+2
;②y=x2-3|x|+2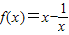 ;②y=x2-3|x|+2
;②y=x2-3|x|+2