题目内容
.已知奇函数f(x)满足f(-1)=f(3)=0,在区间[-2,0)上是减函数,在区间[2,+∞)是增函数,函数F(x)=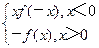 ,则{x|F(x)>0}=
,则{x|F(x)>0}=
| A.{x|x<-3,或0<x<2,或x>3} |
| B.{x|x<-3,或-1<x<0,或0<x<1,或x>3} |
| C.{x|-3<x<-1,或1<x<3} |
| D.{x|x<-3,或0<x<1,或1<x<2,或2<x<3} |
C
解析

练习册系列答案
相关题目
函数 的定义域为
的定义域为
A.  | B.  | C.  | D.  |
设函数f(x)(x∈R)为奇函数,f(1)= ,
, f(x+2)=f(x)+f(2),则f(5)=
f(x+2)=f(x)+f(2),则f(5)=
| A.0 | B.1 | C.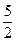 | D.5 |
为了得到函数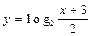 的图象,只需把函数
的图象,只需把函数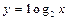 的图象上所有的点( )
的图象上所有的点( )
| A.向左平移3个单位长度,再向上平移1个单位长度 |
B.向右平移3个单位长度,再向上平移1个 单位长度 单位长度 |
| C.向左平移3个单位长度,再向下平移1个单位长度 |
| D.向右平移3个单位长度,再向下平移1个单位长度 |
设实数、y满足约束条件,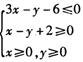 ,若目标函数
,若目标函数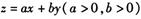 的最大值为12,则
的最大值为12,则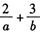 的最小值为()
的最小值为()
| A.4 | B.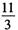 | C.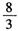 | D.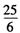 |
三个函数①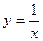 ;②
;②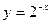 ;③
;③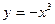 中,在其定义域内是奇函数的个数是( )
中,在其定义域内是奇函数的个数是( )
| A.1 | B.0 | C.3 | D.2 |
在区间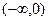 上为增函数的是( )
上为增函数的是( )
A.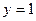 | B.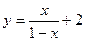 | C.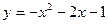 | D.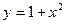 |
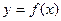 的导函数在区间[a,b]是增函数,则函数
的导函数在区间[a,b]是增函数,则函数