题目内容
已知
是定义域为R的奇函数， 
,的导函数
的图象如图所示， 若两正数
满足
，则
的取值范围是( )
A． | B． | C． | D． |
B
解析试题分析：由图知
，故函数
在R内单调递增，又，且是定义域为R的奇函数，所以
，∴
，∴
，画出点
所在的平面区域，如图所示，
表示可行域内的点和点
连线斜率，则其范围为.
考点：1、导数在单调性上的应用；2、函数的奇偶性；3、线性规划.
练习册系列答案
相关题目
已知O是坐标原点，点
，若点
为平面区域
上的一个动点，则|AM|的最小值是( )
A． | B． | C． | D． |
设
满足约束条件
，则目标函数
的最大值是（ ）
| A．3 | B．4 | C．5 | D．6 |
若变量x,y满足约束条件
则
的最大值为
| A．4 | B．3 | C．2 | D．1 |
设变量
满足约束条件：
，则
的最小值（ ）
A． | B． | C． | D． |
若实数
、
满足不等式组
，则
的最大值为（ ）
A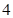． | B． | C． | D． |
若
，且
，则
的最小值等于（ ）
| A．9 | B．5 | C．3 | D．2 |
已知
，
、
满足约束条件
，若
的最小值为
，则
（ ）
A． | B． | C． | D． |
设不等式组
表示的平面区域为D.若指数函数y＝ax的图象上存在区域D上的点，则a的取值范围是( )．
| A．(1,3] | B．[2,3] | C．(1,2] | D．[3，＋∞) |