题目内容
若
=(1,1,x),
=(2,4,2),
=(1,1,1)满足条件(
-
)•
=-2,则x=
| a |
| b |
| c |
| c |
| a |
| b |
2
2
.分析:根据向量
、
的坐标,算出向量
-
的坐标,结合空间向量数量积的坐标公式列出关于x的方程,解之即可得到实数x的值.
| a |
| c |
| c |
| a |
解答:解:∵
=(1,1,x),
=(1,1,1),
∴
-
=(0,0,1-x)
又∵
=(2,4,2),
∴(
-
)•
=-2,即0×2+0×4+(1-x)×2=-2
解之得x=2
故答案为:2
| a |
| c |
∴
| c |
| a |
又∵
| b |
∴(
| c |
| a |
| b |
解之得x=2
故答案为:2
点评:本题给出向量
、
的坐标,求满足(
-
)•
=-2的x值.着重考查了空间向量的坐标运算及数量积的运算等知识,属于基础题.
| a |
| c |
| c |
| a |
| b |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 恒成立,求函数f(x)的解析表达式;
恒成立,求函数f(x)的解析表达式;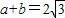 ,证明:
,证明: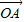 与
与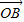 不可能垂直.
不可能垂直.