Question

在地上画一正方形线框，其边长等于一枚硬币的直径的2倍，向方框中投掷硬币，硬币完全落在正方形外的不计，则硬币完全落在正方形内的概率为（　　）

• A．

  1

  4

• B．

  1

  8

• C．

  1

  16

• D．

  4

  32+π

Answer 1

分析：由题意知本题是一个几何概型，概率等于面积之比，根据题意算出试验包含的总面积和符合条件的面积，两者求比值，得到要求的概率．

解答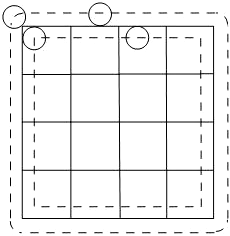：解：设硬币的直径为2cm，正方形线框的边长为4．
考虑圆心的运动情况．
因为每次投掷都落在最大的正方形内或与最大的正方形有公共点，所以圆心的最大限度为原正方形向外再扩张1个小圆半径的区域，且四角为四分之圆弧；
此时总面积为：
4×4+4×4×1+π×1²=32+π；
完全落在最大的正方形内时，圆心的位置在2为边长的正方形内，
其面积为：2×2=4；
∴硬币落下后完全在最大的正方形内的概率为：P=

4

32+π

．
故选D．

点评：本题考查几何概型和求面积的方法，几何概型和古典概型是高中必修中学习的高考时常以选择和填空出现，有时文科会考这种类型的解答题目．