题目内容
设m,n,p均为正数,且3m=log
m,(
)p=log3p,(
)q=log
q,则( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
分析:根据指数函数和对数函数的性质,得到三个数字与0,1之间的大小关系,利用两个中间数字得到结果.
解答:解:∵m>0,故3m>30=1,
∴3m=log
m>1=log
,
∴0<m<
;①
同理,(
)p=log3p>0,
∴p>1;②
∵q>0,(
)q<1,(
)q=log
q>0=log
1,
∴0<q<1;③
由于①与③目前尚不能判断,不妨令q=
,(
)q=(
)
=
,
令x=log
q=log
,则(
)x=
,即3x=2,而3
=
<2,
∴x>
.
∴即当x=
时,函数y=log
x的图象在函数y=(
)x图象的上方,
∴函数y=log
x的图象与函数y=(
)x图象的交点的横坐标即(
)q=log
q中的q>
④
由①②④可得:p>q>m.
故选D.
∴3m=log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴0<m<
| 1 |
| 2 |
同理,(
| 1 |
| 3 |
∴p>1;②
∵q>0,(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴0<q<1;③
由于①与③目前尚不能判断,不妨令q=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
令x=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴x>
| 1 |
| 2 |
∴即当x=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
∴函数y=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
由①②④可得:p>q>m.
故选D.
点评:题考查对数值的大小比较,本题解题的关键是找出一个中间数字,使得三个数字利用中间数字隔开,难点在于m与q大小的比较,属于难题.

练习册系列答案
相关题目
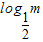 ,(
,( )p=log3p,(
)p=log3p,( )q=
)q=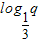 ,则( )
,则( )