题目内容
(2012•通州区一模)已知函数f(x)=2sinxcosx+2cos2x-1.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-
,0]上的最大值和最小值.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-
| π | 2 |
分析:(Ⅰ)根据三角函数的恒等变换化简函数f(x)的解析式为
sin(2x+
),由此求得它的最小正周期.
(Ⅱ) 因为 x∈[-
,0]时,2x+
∈[-
,
],再利用正弦函数的定义域和值域求得函数f(x)在区间[-
,0]上的最大值和最小值.
| 2 |
| π |
| 4 |
(Ⅱ) 因为 x∈[-
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
解答:解:(Ⅰ)∵函数f(x)=2sinxcosx+2cos2x-1=sin2x+cos2x=
sin(2x+
),…(3分)
所以 f(x) 的最小正周期为 π. …(6分)
(Ⅱ) 因为 x∈[-
,0]时,2x+
∈[-
,
],
所以当 2x+
=
,即 x=0 时,sin(2x+
)=
,所以f(x)取得最大值1.
当 2x+
=-
,即 x=-
时,所以f(x)取得最小值-
. …(13分)
| 2 |
| π |
| 4 |
所以 f(x) 的最小正周期为 π. …(6分)
(Ⅱ) 因为 x∈[-
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
所以当 2x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
当 2x+
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
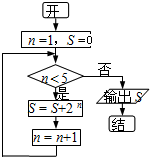 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )