题目内容
定义在
上的奇函数
，
，且对任意不等的正实数
，
都满足
，则不等式
的解集为( ).
A． | B． |
C． | D． |
A
解析试题分析：由
在
单调递增. 又
在上为奇函数，所以在上单调递增. 不等式
当时, 
所以
.
当
时, 
所以
.
所以不等式
的解集为
,故选A
考点：函数的奇偶性,单调性,不等式转化.
练习册系列答案
相关题目
下列函数中，在其定义域中，既是奇函数又是减函数的是（ ）
A． | B． | C． | D． |
函数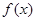
的定义域为
，且满足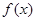：是偶函数，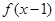
是奇函数，若
，则
（ ）
A． 9 | B．9 | C．3 | D．0 |
满足条件：（1）
、
的图象上，（2）
的图象与函数
的图象中“和谐点对”的个数是（ ）若函数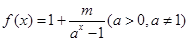
是奇函数，则
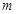为
A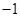． | B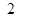． | C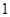． | D． |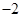
函数
的零点所在的区间是（ ）
A． | B． | C． | D． |
下列函数中,既是偶函数又在
上单调递增的是 ( )
A． | B． | C． | D． |
已知
若
则
等于 （ ）
A． | B． | C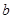． | D． |
已知函数
，若
互不相等，且
，则
的取值范围是（ ）
A． | B． | C． | D． |