题目内容
已知函数![]() 的图象过原点,且关于点
的图象过原点,且关于点![]() 成中心对称.
成中心对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若数列![]() 满足:
满足:![]() ,求
,求![]() ,
,![]() ,
,![]() 的值,猜想数列
的值,猜想数列![]() 的通项公式
的通项公式![]() ,并证明你的结论;
,并证明你的结论;
解析:(1)∵函数![]() 的图象过原点,
的图象过原点,
∴![]() 即
即![]() ,∴
,∴![]() .
.
又函数![]() 的图象关于点
的图象关于点![]() 成中心对称,
成中心对称,
∴![]() ,
,![]() .
.
(2)解:由题意有 即
即 ,
,
即![]() ,即
,即![]() .
.
∴数列{![]() }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.
∴![]() ,即
,即![]() . ∴
. ∴![]() .
.
∴ ![]() ,
,![]() ,
,![]() ,
,![]() .
.
(3)证明:当![]() 时,
时,![]()
![]()
故 ![]()

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称. ,求数列an的通项公式an.
,求数列an的通项公式an. 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.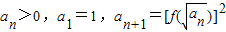 ,求数列an的通项公式an.
,求数列an的通项公式an.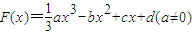 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B. ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.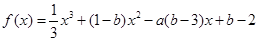 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组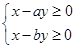 所确定的平面区域在
所确定的平面区域在 内的面积为 .
内的面积为 .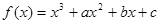 的图象过原点,且
的图象过原点,且 在
在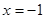 ,
, 处取得极值.
处取得极值.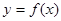 与
与 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.