题目内容
在a>0,b>0的条件下,四个结论:①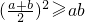 ,②
,②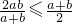 ,③
,③ ,④
,④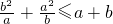 ;其中正确的个数是
;其中正确的个数是
- A.1
- B.2
- C.3
- D.4
C
分析:欲证明②③:“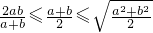 ”,即要证明两个不等式:“
”,即要证明两个不等式:“ ”对于前一个可直接利用作差法;对于后一个先将两边的式子平方后再利用作差的方法,作差后结合基本不等式进行证明即得.
”对于前一个可直接利用作差法;对于后一个先将两边的式子平方后再利用作差的方法,作差后结合基本不等式进行证明即得.
对于①平方后化简即为基本不等式;对于④,通过取特殊值可知其正确与否.
解答:对于②③:因为a>0,b>0
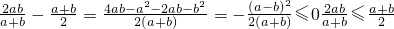 ,
,
当且仅当a=b时取等号.(5分)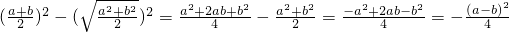
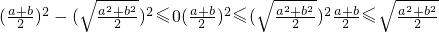 ,
,
当且仅当a=b时取等号.(11分)
综上知: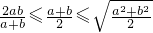 ,当且仅当a=b时等号成立;
,当且仅当a=b时等号成立;
①:由于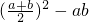 =
=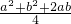 =
=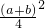 ≥0,成立,故 ①正确.
≥0,成立,故 ①正确.
④:取a=2,b=1,代入可知其不成立.
故选C.
点评:本题主要考查了不等式的证明方法,主要方法有:作差法,分析法,综合法都可,作差法是指:应用数的减法运算可以比较两个数的大小,这就是“作差法”,既要比较两个数a与b的大小,可先求出a与b的差a-b与0比较即可.
分析:欲证明②③:“
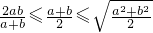 ”,即要证明两个不等式:“
”,即要证明两个不等式:“ ”对于前一个可直接利用作差法;对于后一个先将两边的式子平方后再利用作差的方法,作差后结合基本不等式进行证明即得.
”对于前一个可直接利用作差法;对于后一个先将两边的式子平方后再利用作差的方法,作差后结合基本不等式进行证明即得.对于①平方后化简即为基本不等式;对于④,通过取特殊值可知其正确与否.
解答:对于②③:因为a>0,b>0
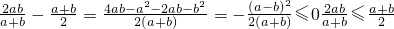 ,
,当且仅当a=b时取等号.(5分)
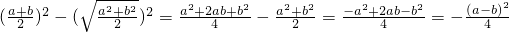
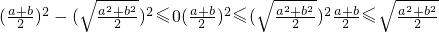 ,
,当且仅当a=b时取等号.(11分)
综上知:
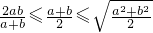 ,当且仅当a=b时等号成立;
,当且仅当a=b时等号成立;①:由于
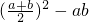 =
=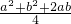 =
=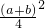 ≥0,成立,故 ①正确.
≥0,成立,故 ①正确.④:取a=2,b=1,代入可知其不成立.
故选C.
点评:本题主要考查了不等式的证明方法,主要方法有:作差法,分析法,综合法都可,作差法是指:应用数的减法运算可以比较两个数的大小,这就是“作差法”,既要比较两个数a与b的大小,可先求出a与b的差a-b与0比较即可.

练习册系列答案
相关题目
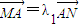 ,
,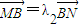 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.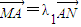 ,
,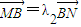 ,问λ1+λ2是否为定值?说明理由.
,问λ1+λ2是否为定值?说明理由.