题目内容
3.若实数x,y满足3x+1≥ex+y-3+e2x-y+2则x+y=3.分析 根据[(x+y-3)+1]≤ex+y-3,[(2x-y+2)+1]≤e2x-y+2,得到$\left\{\begin{array}{l}{x+y-2{≤e}^{x+y-3}}\\{2x-y+3{=e}^{2x-y+2}}\end{array}\right.$,求出x,y的值即可.
解答 解:令f(x)=ex-(x+1),
则f′(x)=ex-1,
令f′(x)>0,解得:x>0,
令f′(x)<0,解得:x<0,
故f(x)的最小值是f(0)=0,
故ex≥x+1,
∵3x+1≥ex+y-3+e2x-y+2,
∴[(x+y-3)+2]+[(2x-y+2)+1]
≥ex+y-3+e2x-y+2,
即[(x+y-3)+1]≤ex+y-3,[(2x-y+2)+1]≤e2x-y+2,
∴$\left\{\begin{array}{l}{x+y-2{≤e}^{x+y-3}}\\{2x-y+3{=e}^{2x-y+2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x+y-3=0}\\{2x-y+2=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{8}{3}}\end{array}\right.$,
∴x+y=3,
故答案为:3.
点评 本题考查了不等式的性质,考查转化思想,是一道综合题.

练习册系列答案
相关题目
14.根据下表提供的数据,由散点图可知,y与x具有较好的线性相关关系,其线性回归方程为$\widehat{y}$=-0.7x+5.25,那么表中t的值为( )
| x | 1 | 2 | 3 | 4 |
| y | 4.5 | 4 | t | 2.5 |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
18.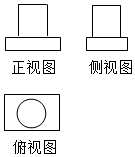 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )| A. | 两个长方体 | B. | 两个圆柱 | ||
| C. | 一个长方体和一个圆柱 | D. | 一个球和一个长方体 |
8. 如图,在△ABC中,D为线段BC的中点,E,F,G依次为线段AD从上至下的3个四等分点,若$\overrightarrow{AB}$+$\overrightarrow{AC}$=4$\overrightarrow{AP}$,则( )
如图,在△ABC中,D为线段BC的中点,E,F,G依次为线段AD从上至下的3个四等分点,若$\overrightarrow{AB}$+$\overrightarrow{AC}$=4$\overrightarrow{AP}$,则( )
 如图,在△ABC中,D为线段BC的中点,E,F,G依次为线段AD从上至下的3个四等分点,若$\overrightarrow{AB}$+$\overrightarrow{AC}$=4$\overrightarrow{AP}$,则( )
如图,在△ABC中,D为线段BC的中点,E,F,G依次为线段AD从上至下的3个四等分点,若$\overrightarrow{AB}$+$\overrightarrow{AC}$=4$\overrightarrow{AP}$,则( )| A. | 点P与图中的点D重合 | B. | 点P与图中的点E重合 | ||
| C. | 点P与图中的点F重合 | D. | 点P与图中的点G重合 |
15. 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )| A. | $\frac{π}{2}+1$ | B. | $\frac{π}{2}+3$ | C. | $\frac{3π}{2}+1$ | D. | $\frac{3π}{2}+3$ |
18.设集合U={1,2,3,4,5,6,7},集合A={1,2,5,7},则∁UA=( )
| A. | {1,2,5,7} | B. | {3,4,6} | C. | {6} | D. | U |