题目内容
函数F(x)=xf(x)(x∈R)在(-∞,0)上是减函数,且f(x)是奇函数,则对任意实数a,下列不等式成立的是
- A.
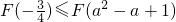
- B.
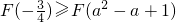
- C.
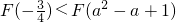
- D.
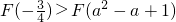
A
分析:首先判断出F(x)的是偶函数,然后根据函数F(x)=xf(x)(x∈R)在(-∞,0)上是减函数,则知函数F(x)=xf(x)x∈R,在(0,+∞)上是增函数,再比较 和a2-a+1的大小,根据函数的单调性即可得到答案.
和a2-a+1的大小,根据函数的单调性即可得到答案.
解答:∵y=x是奇函数,f(x)是奇函数,
∴函数F(x)=xf(x)是偶函数,
∴F(- )=F(
)=F( ),
),
∵函数F(x)=xf(x)(x∈R)在(-∞,0)上是减函数,
∴函数F(x)=xf(x)(x∈R)在(0,+∞)上是增函数,
∵a2-a+1= +
+ ≥
≥ ,
,
∴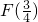 ≤F(a2-a+1),
≤F(a2-a+1),
∵F(- )=F(
)=F( ),
),
∴F(- )≤F(a2-a+1),
)≤F(a2-a+1),
故选A.
点评:本题主要考查奇函数和函数单调性的应用的知识,解答本题的关键是能判断出函数F(x)的奇偶性,本题难度一般.
分析:首先判断出F(x)的是偶函数,然后根据函数F(x)=xf(x)(x∈R)在(-∞,0)上是减函数,则知函数F(x)=xf(x)x∈R,在(0,+∞)上是增函数,再比较
 和a2-a+1的大小,根据函数的单调性即可得到答案.
和a2-a+1的大小,根据函数的单调性即可得到答案.解答:∵y=x是奇函数,f(x)是奇函数,
∴函数F(x)=xf(x)是偶函数,
∴F(-
 )=F(
)=F( ),
),∵函数F(x)=xf(x)(x∈R)在(-∞,0)上是减函数,
∴函数F(x)=xf(x)(x∈R)在(0,+∞)上是增函数,
∵a2-a+1=
 +
+ ≥
≥ ,
,∴
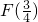 ≤F(a2-a+1),
≤F(a2-a+1),∵F(-
 )=F(
)=F( ),
),∴F(-
 )≤F(a2-a+1),
)≤F(a2-a+1),故选A.
点评:本题主要考查奇函数和函数单调性的应用的知识,解答本题的关键是能判断出函数F(x)的奇偶性,本题难度一般.

练习册系列答案
相关题目