题目内容
如图，点L，M，N分别为△ABC三边BC，CA，AB上的点，且| BL |
| BC |
| AM |
| CA |
| AN |
| AB |
| AL |
| BM |
| CN |
分析：选定好基底，利用向量共线的充要条件将
，
用基底表示，再利用向量的运算法则将
、
、
用基底表示，
代入已知等式，求出系数的关系．
| BL |
| CM |
| AL |
| BM |
| CN |
代入已知等式，求出系数的关系．
解答：证明：设
=
，
=
为基底，
由已知得
=l
，
=m
，
∵
=
+
=-
-
，∴
=n
=-n
-n
，
∴
=
+
=(l-1)
-
①
=
+
=
+m
②
=
+
=-n
+(1-n)
③
将①②③代入
+
+
=0，得，(l-n)
+(m-n)
=0
∴l=m=n．
| BC |
| a |
| CA |
| b |
由已知得
| BL |
| a |
| CM |
| b |
∵
| AB |
| AC |
| CB |
| a |
| b |
| AN |
| AB |
| a |
| b |
∴
| AL |
| AB |
| BL |
| a |
| b |
| BM |
| BC |
| CM |
| a |
| b |
| CN |
| CA |
| AN |
| a |
| b |
将①②③代入
| AL |
| BM |
| CN |
| a |
| b |
∴l=m=n．
点评：本题考查向量关共线的充要条件、利用平面向量基本定理将向量用基底线性表示．
练习册系列答案
相关题目
如图，在棱长为a的正方体ABCD-A1B1C1D1中，M、N分别是AA1、D1C1的中点，过D、M、N三点的平面与正方体的下底面相交于直线l；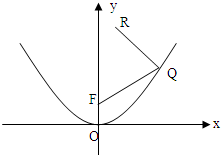
如图所示，F是抛物线x2=2py（p＞0）的焦点，点R（1，4）为抛物线内一定点，点Q为抛物线上一动点，|QR|+|QF|的最小值为5．
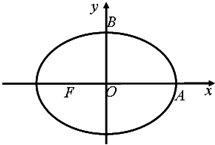如图，点F是椭圆W：
