题目内容
设a＞0，a≠1，函数f(x)=
，
，且f(2
)=1，则f（f（2））=
|
|
| 2 |
6
6
．分析：由a＞0，a≠1，f(x)=
，
，且f(2
)=1，解得a=7．故f（2）=log73，由此能求出f（f（2））．
|
|
| 2 |
解答：解：∵a＞0，a≠1，
f(x)=
，
，且f(2
)=1，
∴loga（8-1）=1，∴a=7．
∴f（2）=log73，
∴f（f（2））=f（log73）=2×7log73=6．
故答案为：6．
f(x)=
|
|
| 2 |
∴loga（8-1）=1，∴a=7．
∴f（2）=log73，
∴f（f（2））=f（log73）=2×7log73=6．
故答案为：6．
点评：本题考查分段函数的函数值的求法，解题时要认真审题，仔细解答，注意对数性质的灵活运用．
练习册系列答案
相关题目
的定义域为R，若存在与
无关的正常数M，使
对一切实数
；
；
；
．其中是“有界泛函”的个数为 （ ）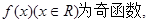
（ ）
D．5
的定义域为R，若存在与
无关的正常数M，使
对一切实数
；
；
；
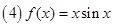．其中是“有界泛函”的个数为 （ ）
)的定义域为R，若存在与
对一切实数
②f(
④
其中是“有界泛函”的个数为（
）
对一切实数x均成立，则称f(x)为“有界泛函”，给出以下函数：①f(x) =x2，②f(x)=2x，③
其中是“有界泛函”的个数为