题目内容
.已知数列{an}满足:an+1=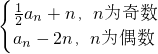 ,
,
(Ⅰ)求a2•a3;
(Ⅱ)设bn=a2n-2,n∈N*,求证:数列{bn}是等比数列,并求其通项公式;
(Ⅲ)求数列{an}前100项中所有奇数项的和.
(Ⅰ)解:a1=1,n=1时,a2= a1+1=
a1+1= ;n=2时,a3=a2-4=
;n=2时,a3=a2-4= ;
;
∴a2•a3=-
(Ⅱ)证明:b1=a2-2=- ,且
,且 =
= =
= =
=
∴数列{bn}是以 为首项,
为首项, 为公比的等比数列;
为公比的等比数列;
∴
 =-
=-
(Ⅲ)解:由(Ⅱ)得
∵当n=2k时,a2k+1=a2k-2×2k(k=1,2…,49)
∴数列{an}前100项中所有奇数项的和为1-2×(2+4+…+98)+a2+a4+…+a98=
分析:(Ⅰ)a1=1,利用数列递推式,n=1时,a2= a1+1=
a1+1= ;n=2时,a3=a2-4=
;n=2时,a3=a2-4= ;故可求a2•a3的值;
;故可求a2•a3的值;
(Ⅱ)b1=a2-2=- ,且
,且 =
= =
= =
= ,故可得数列{bn}是以
,故可得数列{bn}是以 为首项,
为首项, 为公比的等比数列,从而可求其通项公式;
为公比的等比数列,从而可求其通项公式;
(Ⅲ)由(Ⅱ)得 ,当n=2k时,a2k+1=a2k-2×2k(k=1,2…,49),从而可求数列{an}前100项中所有奇数项的和.
,当n=2k时,a2k+1=a2k-2×2k(k=1,2…,49),从而可求数列{an}前100项中所有奇数项的和.
点评:本题考查数列的递推式,考查等比数列的定义,考查数列的求和,解题的关键是构造新数列,属于中档题.
 a1+1=
a1+1= ;n=2时,a3=a2-4=
;n=2时,a3=a2-4= ;
;∴a2•a3=-

(Ⅱ)证明:b1=a2-2=-
 ,且
,且 =
= =
= =
=
∴数列{bn}是以
 为首项,
为首项, 为公比的等比数列;
为公比的等比数列;∴

 =-
=-
(Ⅲ)解:由(Ⅱ)得

∵当n=2k时,a2k+1=a2k-2×2k(k=1,2…,49)
∴数列{an}前100项中所有奇数项的和为1-2×(2+4+…+98)+a2+a4+…+a98=

分析:(Ⅰ)a1=1,利用数列递推式,n=1时,a2=
 a1+1=
a1+1= ;n=2时,a3=a2-4=
;n=2时,a3=a2-4= ;故可求a2•a3的值;
;故可求a2•a3的值;(Ⅱ)b1=a2-2=-
 ,且
,且 =
= =
= =
= ,故可得数列{bn}是以
,故可得数列{bn}是以 为首项,
为首项, 为公比的等比数列,从而可求其通项公式;
为公比的等比数列,从而可求其通项公式;(Ⅲ)由(Ⅱ)得
 ,当n=2k时,a2k+1=a2k-2×2k(k=1,2…,49),从而可求数列{an}前100项中所有奇数项的和.
,当n=2k时,a2k+1=a2k-2×2k(k=1,2…,49),从而可求数列{an}前100项中所有奇数项的和.点评:本题考查数列的递推式,考查等比数列的定义,考查数列的求和,解题的关键是构造新数列,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目