题目内容
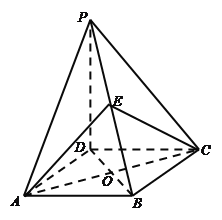
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,现沿对角线
,现沿对角线![]() 将
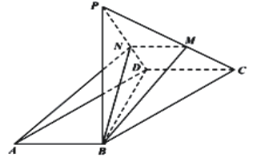
将![]() 折起,使点A到达点P,点M,N分别在直线
折起,使点A到达点P,点M,N分别在直线![]() ,
,![]() 上,且A,B,M,N四点共面.
上,且A,B,M,N四点共面.
(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,二面角
,二面角![]() 平面角大小为
平面角大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据余弦定理,可得![]() ,利用
,利用![]() //
//![]() ,可得
,可得![]() //平面
//平面![]() ,然后利用线面平行的性质定理,
,然后利用线面平行的性质定理,![]() //
//![]() ,最后可得结果.
,最后可得结果.
(2)根据二面角![]() 平面角大小为
平面角大小为![]() ,可知N为
,可知N为![]() 的中点,然后利用建系,计算
的中点,然后利用建系,计算![]() 以及平面
以及平面![]() 的一个法向量,利用向量的夹角公式,可得结果.
的一个法向量,利用向量的夹角公式,可得结果.
(1)不妨设![]() ,则
,则![]() ,
,
在![]() 中,
中,
![]() ,
,
则![]() ,
,
因为![]() ,
,
所以![]() ,因为
,因为![]() //
//![]() ,
,
且A、B、M、N四点共面,所以![]() //平面
//平面![]() .
.
又平面![]() 平面
平面![]() ,所以
,所以![]() //
//![]() .
.
而![]() ,
,![]() .
.
(2)因为平面![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,
,
因为![]() ,平面
,平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,
,
所以![]() ,在
,在![]() 中,易知N为
中,易知N为![]() 的中点,
的中点,
如图,建立空间直角坐标系,
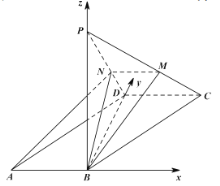
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由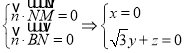 ,
,
令![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则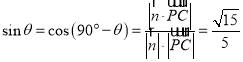 .
.

练习册系列答案
相关题目
【题目】针对某新型病毒,某科研机构已研发出甲乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有![]() 的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占
的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占![]() .
.
产生抗体 | 未产生抗体 | 合计 | |
甲 | |||
乙 | |||
合计 |
(1)根据题中数据,完成列联表;
(2)根据(1)中的列联表,判断能否有![]() 的把握认为甲乙两种疫苗的效果有差异.
的把握认为甲乙两种疫苗的效果有差异.
参考公式: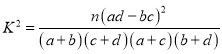 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|