题目内容
给出下列α所属的四个区间，能使sinα＞tanα＞
成立的是（ ）
| 1 |
| tanα |
A、（-
| ||||
B、（-
| ||||
C、（0，
| ||||
D、（
|
分析：利用排除法，结合选项中所给的区间上任取一值，代入验证是否满足sinα＞tanα＞
，从而排除错误选项即可
| 1 |
| tanα |
解答：解：A在区间(-
π，-
)取α=-
，则tan(-
)=-
＜
，故A错误；
B成立；
C：在区间(0，
)上取α=
，则sinα=
＜
=tanα，故C错误
D：在区间(
，
)上取α=
，则sinα=
＜
=tanα，故D错误
故选B
| 1 |
| 2 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 1 | ||
tan(-
|
B成立；
C：在区间(0，
| π |
| 4 |
| π |
| 6 |
| 1 |
| 2 |
| ||
| 3 |
D：在区间(
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
| 3 |
故选B
点评：本题主要考查了三角函数值的大小的比较，结合选择题的特点，采用排除法既可以减少运算量，又可以快速、准确的找出选项．
练习册系列答案
相关题目
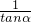成立的是
，-
）
成立的是（ ）
，-
）
，0）
）
，
）
，
） 
，0） 
） 
，
）