题目内容
若三棱锥S-ABC的顶点S在底面上的射影H在△ABC的内部,且是△ABC的垂心,则( )
| A.三条侧棱长相等 |
| B.三个侧面与底面所成的角相等 |
| C.H到△ABC三边的距离相等 |
| D.点A在平面SBC上的射影是△SBC的垂心 |

∵三棱锥S-ABC的顶点S在底面的射影H是△ABC的垂心,
∴三棱锥的三条相对的棱两两垂直,
反之,若三棱锥的三条相对的棱两两垂直,
则有三棱锥任意一个顶点在对面的射影是对面三角形的垂心,
过顶点A向平面SBC作垂线,垂足为H,如图,
根据线面垂直的性质定理,得到垂足H是△SBC的高线的交点,
∴点A在平面SBC上的射影必是△SBC的垂心,
故选D.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 B.
B. C.
C. D.
D.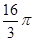
 ABC中,两直角边分别为a,b,斜边上的高为h,则得
ABC中,两直角边分别为a,b,斜边上的高为h,则得 ”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.