题目内容
已知双曲线![]() -
-![]() =1(a>0,b>0)左、右焦点分别为F1和F2,P是它左侧分支上一点,P点到左准线距离为d.
=1(a>0,b>0)左、右焦点分别为F1和F2,P是它左侧分支上一点,P点到左准线距离为d.
(1)若y=![]() x是已知双曲线的一条渐近线,是否存在点P,使d,|PF1|,|PF2|成等比数列?若不存在,说明理由.
x是已知双曲线的一条渐近线,是否存在点P,使d,|PF1|,|PF2|成等比数列?若不存在,说明理由.
(2)在已知双曲线的左分支上,使d,|PF1|,|PF2|成等比数列的点P存在时,求离心率e的取值范围.
答案:
解析:
解析:
|
解:(1)由已知得b= ∴e=2.假设存在P(x,y),使d,|PF1|,|PF2|成等比数列. 又d=-x- ∵P是双曲线左支上的点,∴x≤-a,∴x=- 代入 ∴y=± ∴点P存在,其坐标为(- (2)解法一:设存在P(x0,y0)且x0≤-a,使d,|PF1|,|PF2|成等比数列, 即|PF1|2=d·|PF2|.由双曲线第二定义得 ∴|PF1|=ed,∴(ed)2=d· ∴e(- ∵x0≤-a,∴ ∴e2-2e-1≤0,∴1- 又e>1,∴1<e≤ 解法二:由解法一得|PF2|=e|PF1|,又|PF2|-|PF1|=2a, ∴|PF1|< ∵|PF1|+|PF2|≥|F1F2|. ∴ 得1<e≤ |

练习册系列答案
相关题目
 .
. ≤-a,
≤-a,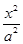 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e= ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
. ·
· =-23,求直线m的方程.
=-23,求直线m的方程. -
- =1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P,使=,求双曲线的离心率的范围.
=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P,使=,求双曲线的离心率的范围. -
- =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(
)
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是(
)