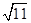题目内容
点B是点A(1,2,3)在坐标面xOy内的射影,其中O为坐标原点,则|
|等于 .
| OB |
分析:根据点B是A(1,2,3)在xOy坐标平面内的射影,所以A与B的横坐标和竖坐标相同,纵坐标为0,得到B的坐标,根据两点之间的距离公式得到结果.
解答:解:∵点B是A(1,2,3)在xOy坐标平面内的射影,
∴B点的坐标是(1,2,0),
∴|
|=
=
,
故答案为:
.
∴B点的坐标是(1,2,0),
∴|
| OB |
| 12+22+02 |
| 5 |
故答案为:
| 5 |
点评:本题考查空间直角坐标系,考查空间中两点间的距离公式,是一个基础题,解题的关键是,一个点在一个坐标平面上的射影的坐标同这个点的坐标的关系.

练习册系列答案
相关题目
点B是点A(1,2,3)在坐标平面yOz内的正投影,则|OB|等于( )
A、
| ||
B、
| ||
C、2
| ||
D、
|
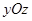 内的射影,则OB等于 ( )
内的射影,则OB等于 ( )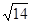 B.
B.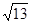 C.
C.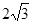 D.
D.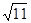
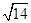 B、
B、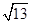
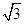 D、
D、