Question

【题目】已知抛物线 上的点 到焦点 的距离为 ．

（1）求 ， 的值；
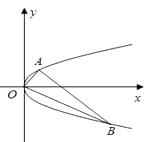
（2）设 ， 是抛物线上分别位于 轴两侧的两个动点，且 （其中 为坐标原点）．求证：直线 过定点，并求出该定点的坐标．

Answer 1

【答案】
（1）解：由抛物线的定义得， ，解得 ，

所以抛物线的方程为 ，代入点 ，可解得

（2）解：设直线 的方程为 ， ， ，

联立 消元得 ，则 ， ，

由 ，得 ，所以 或 （舍去），

即 ，即 ，所以直线 的方程为 ，

所以直线 过定点

【解析】(1)由题意结合抛物线上的点几何意义可求出P的值，因为点T在抛物线上故把点的坐标满足方程代入求解出t的值即可。(2)首先设出两点的坐标联立直线和抛物线方程消元得到关于x的方程，再借助韦达定理求出两根之和与两根之积的代数式，根据向量的数量积坐标公式解出 y 1y2 的值进而求出n的值故得出直线过定点。