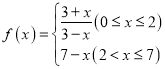题目内容
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为 ![]() .
.
(1)求 ![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 ![]() 的图象,若关于
的图象,若关于 ![]() 的方程
的方程 ![]() 在区间
在区间 ![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)[
;(2)[![]() ]
]
【解析】
⑴利用三角函数的恒等变换化简函数![]() 的表达式为
的表达式为![]() ,再根据
,再根据![]() 的最小正周期
的最小正周期![]() 求得
求得![]() 的值,从而得到
的值,从而得到![]() 的表达式
的表达式
⑵根据函数![]() 的图象变换规律,可得
的图象变换规律,可得![]() ,由题意可得
,由题意可得![]() 与
与![]() 在区间
在区间![]() 上有解,结合正弦函数的图像求得答案
上有解,结合正弦函数的图像求得答案
(1)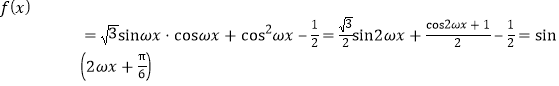
又![]() 的最小正周期
的最小正周期![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() .
.
(2)将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,得到
个单位长度后,得到![]() 的图象;再将所得图象上所有点的横坐标伸长到原来的
的图象;再将所得图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变)得到
倍(纵坐标不变)得到![]() 的图象,
的图象,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
易知当![]() ,即
,即 ![]() 时,
时,![]() 递增,且
递增,且![]() ,
,
当![]() ,即
,即 ![]() 时,
时,![]() 递减,且
递减,且![]() .
.
又![]() 在区间
在区间![]() 上有实数解,
上有实数解,
即函数![]() 与
与![]() 的图象在区间
的图象在区间 ![]() 上有交点,
上有交点,
所以![]() 。
。
解得![]() 所以实数
所以实数![]() 的取值范围是[
的取值范围是[![]() ]
]

 应用题作业本系列答案
应用题作业本系列答案【题目】汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,![]() 表示反应距离,
表示反应距离,![]() 表示制动距离,则
表示制动距离,则![]() .下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
.下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
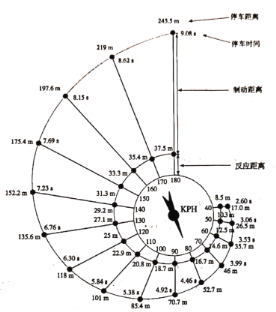
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型一:![]() 或模型二:
或模型二:![]() (其中v为汽车速度,a,b
(其中v为汽车速度,a,b
(2)通过计算![]() 时的停车距离,分析选择哪一个函数模型的拟合效果更好.
时的停车距离,分析选择哪一个函数模型的拟合效果更好.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式:  ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.