题目内容
异面直线
AC与BD间的公垂线段AB=4,又AC=2,BD=3,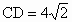 ,求:
,求:
(1)
点C到平面ABD的距离;(2)
两异面直线AB与CD间的距离.
答案:略
解析:
解析:
|
解题思路: (1)如下图所示,作AE BD,连DE,则ABDE是矩形且AB⊥平面ACE.则平面ABDE⊥平面ACE,作CM⊥AE于M,则CM⊥面ABDE,则C点到平面ABD的距离等于CM的长,易知DE⊥EC,DE=AB=4, BD,连DE,则ABDE是矩形且AB⊥平面ACE.则平面ABDE⊥平面ACE,作CM⊥AE于M,则CM⊥面ABDE,则C点到平面ABD的距离等于CM的长,易知DE⊥EC,DE=AB=4, ,则CE=4.又因为AE=BD=3,AC=2,则 ,则CE=4.又因为AE=BD=3,AC=2,则 , , . .
则 ∴ C到面ABD距离为 . .
(2) 由(1)知AB∥ED,则AB∥平面CDE,则AB与CD间距离等于A到平面CDE的距离d,又面ACE⊥面CDE,作AN⊥CE于N.则AN⊥面CDE,则d=AN,在△ ACE中, .∴异面直线AB、CD间的距离为 .∴异面直线AB、CD间的距离为 . . |

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目

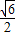 ;④AC垂直于截面BDE.
;④AC垂直于截面BDE.