题目内容
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥DC,已知BD=2AD=2PD=8,AB=2DC=4 .
.

(Ⅰ)设M是PC上一点,证明:平面MBD⊥平面PAD;
(Ⅱ)若M是PC的中点,求棱锥P-DMB的体积.
【答案】
(Ⅰ)详见解析;(Ⅱ)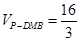 .
.
【解析】
试题分析:(Ⅰ)要证明平面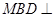 平面
平面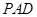 ,只需证明一个平面过另一个平面的垂线,因为M是PC上一点,不确定,故证明
,只需证明一个平面过另一个平面的垂线,因为M是PC上一点,不确定,故证明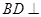 平面
平面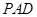 ,显然易证;(Ⅱ)求棱锥P-DMB的体积,直接求,底面面积及高都不好求,但注意到棱锥P-DMB是棱锥P-DCB除去一个小棱锥M-DCB而得到,而这两个棱锥的体积都容易求,值得注意的是,当一个几何体的体积不好求时,可进行转化成其它几何体来求.
,显然易证;(Ⅱ)求棱锥P-DMB的体积,直接求,底面面积及高都不好求,但注意到棱锥P-DMB是棱锥P-DCB除去一个小棱锥M-DCB而得到,而这两个棱锥的体积都容易求,值得注意的是,当一个几何体的体积不好求时,可进行转化成其它几何体来求.
试题解析:(I)证明:在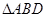 中,由于
中,由于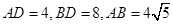 ,所以
,所以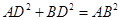 .故
.故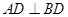 。又平面
。又平面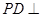 平面
平面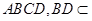 平面
平面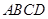 ,所以
,所以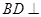 平面
平面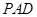 ,又
,又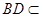 平面
平面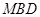 ,故平面
,故平面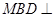 平面
平面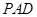 ;
;
(II)过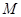 作
作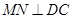 于
于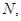
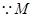 是
是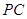 的中点,
的中点,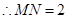 ,
, .
.
考点:本小题考查面面垂直的判定、线面垂直的判定,面面垂直的性质定理应用;,以及棱锥的体积公式,考查学生的化归与转化能力以及空间想象能力.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD= 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.