题目内容
(本小题满分13分)
已知空间向量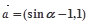 ,
,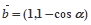 ,
,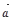 ·
·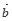 =
= ,
,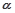 ∈(0,
∈(0,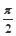 ).
).
(1)求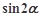 及
及 ,
, 的值;
的值;
(2)设函数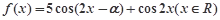 ,求
,求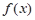 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标;
(3)求函数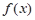 在区间
在区间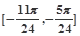 上的值域.
上的值域.
已知空间向量
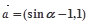 ,
,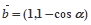 ,
,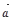 ·
·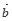 =
= ,
,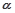 ∈(0,
∈(0,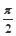 ).
).(1)求
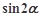 及
及 ,
, 的值;
的值;(2)设函数
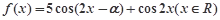 ,求
,求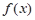 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标;(3)求函数
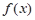 在区间
在区间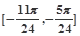 上的值域.
上的值域.(1) ,
,
(2)图象的对称中心为:

(3)当x
 ,2x+
,2x+ ,∴
,∴
∴f(x)的值域为[
 ,
,
(2)图象的对称中心为:


(3)当x

 ,2x+
,2x+ ,∴
,∴
∴f(x)的值域为[

本试主要是考查了向量的数量积公式以及三角函数的性质的综合运用。
(1)结合向量的数量积公式我们分析得到第一问中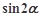 及
及 ,
, 的值;
的值;
(2)根据已知的角和函数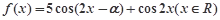 化为单一三角函数,求解周期和对称中心的坐标。
化为单一三角函数,求解周期和对称中心的坐标。
(3)在第二问的基础上利用单调性求解值域。
解:(1)∵
∴ ①
①
∴
∴ ②
②
联立①,②解得:
(2)




令

图象的对称中心为:

(3)当x
 ,2x+
,2x+ ,∴
,∴
∴f(x)的值域为[
(1)结合向量的数量积公式我们分析得到第一问中
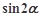 及
及 ,
, 的值;
的值;(2)根据已知的角和函数
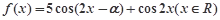 化为单一三角函数,求解周期和对称中心的坐标。
化为单一三角函数,求解周期和对称中心的坐标。(3)在第二问的基础上利用单调性求解值域。
解:(1)∵

∴
 ①
①∴

∴
 ②
②联立①,②解得:

(2)





令


图象的对称中心为:


(3)当x

 ,2x+
,2x+ ,∴
,∴
∴f(x)的值域为[


练习册系列答案
相关题目
 :
: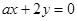 的方向向量是
的方向向量是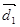 ,直线
,直线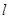 2 :
2 :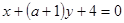 的法向量是
的法向量是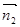 ,若
,若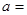 _________.
_________.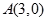 ,
, ,
,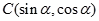 ,其中
,其中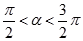 ,
,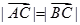 ,求
,求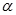 的值
的值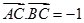 ,求
,求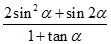 的值
的值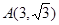 ,O为坐标原点,点P(x,y)的坐标x,y满足
,O为坐标原点,点P(x,y)的坐标x,y满足 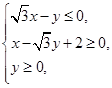
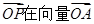 方向上的投影的取值范围是
方向上的投影的取值范围是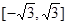
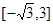
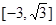
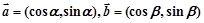 且
且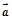 与
与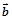 满足关系式:
满足关系式: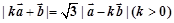 .
.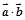 ;
;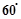 时,求k的值.
时,求k的值. 中,
中, ,
, ,已知点
,已知点 是
是 ,则
,则  .
.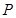 是单位正方体
是单位正方体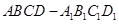 中异于点
中异于点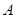 的一个顶点,则
的一个顶点,则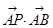 的值为( )
的值为( )  中,若
中,若 =
= ,则
,则

 ,则
,则


