题目内容
函数f(x)=lnx-
的零点个数为( )
| 1 |
| x |
| A.0 | B.1 | C.2 | D.3 |
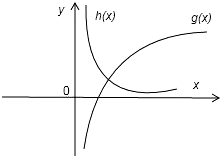
∵f(x)=lnx-
| 1 |
| x |
∴令g(x)=lnx,h(x)=
| 1 |
| x |
g(x)与h(x)只能有一个交点,
故函数f(x)只能有一个零点.
故选B.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
题目内容
| 1 |
| x |
| A.0 | B.1 | C.2 | D.3 |

| 1 |
| x |
| 1 |
| x |

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案