题目内容
( 14分)在数列 ,
, 中,
中, ,
, 且
且 ,
, ,
, 成等差数列,
成等差数列, ,
, ,
, 成等比数列(
成等比数列( )
)
(1)求 ,
, ,
, 及
及 ,
, ,
, ,
,
(2)由(1)猜测数列 ,
, 的通项公式,并用数学归纳法证明你的结论;
的通项公式,并用数学归纳法证明你的结论;
 ,
, 中,
中, ,
, 且
且 ,
, ,
, 成等差数列,
成等差数列, ,
, ,
, 成等比数列(
成等比数列( )
)(1)求
 ,
, ,
, 及
及 ,
, ,
, ,
,(2)由(1)猜测数列
 ,
, 的通项公式,并用数学归纳法证明你的结论;
的通项公式,并用数学归纳法证明你的结论;(1)
(2)猜测 用数学归纳法证明 (见解析).
用数学归纳法证明 (见解析).

(2)猜测
 用数学归纳法证明 (见解析).
用数学归纳法证明 (见解析). (1)由题意得 把
把 分别代入可求得
分别代入可求得
(2)根据前几项的规律,易猜到 用数学归纳法证明时一定要用归纳假设的结论.
用数学归纳法证明时一定要用归纳假设的结论.
由条件得 由此可得
由此可得

猜测
用数学归纳法证明:①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即 那么当n=k+1时,
那么当n=k+1时,

所以当n=k+1时,结论也成立.
由①②,可知 对一切正整数都成立.
对一切正整数都成立.
 把
把 分别代入可求得
分别代入可求得
(2)根据前几项的规律,易猜到
 用数学归纳法证明时一定要用归纳假设的结论.
用数学归纳法证明时一定要用归纳假设的结论.由条件得
 由此可得
由此可得
猜测

用数学归纳法证明:①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即
 那么当n=k+1时,
那么当n=k+1时,
所以当n=k+1时,结论也成立.
由①②,可知
 对一切正整数都成立.
对一切正整数都成立. 
练习册系列答案
相关题目
 中,设
中,设 ,
, ,则
,则 与
与 的大小关系为 。
的大小关系为 。  是首项为1的等比数列,
是首项为1的等比数列, 是
是 ,则数列
,则数列 的前5项和为( )
的前5项和为( ) 或5
或5
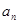 }的前n项和为
}的前n项和为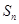 ,若
,若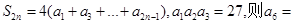
 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则 .
. 的各项均为正数,公比q=2,且
的各项均为正数,公比q=2,且 ,则
,则
 }为递增等比数列,
}为递增等比数列, 和
和 是方程4x2—8x+3=0的两根,则
是方程4x2—8x+3=0的两根,则 =( )
=( )
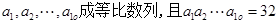 记
记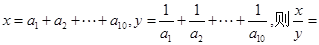
 中,若
中,若 ,
, ,则
,则 的值为 .
的值为 .