题目内容
已知定义在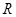 上的函数
上的函数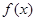 满足
满足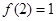 ,且
,且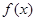 的导函数
的导函数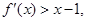 则不等式
则不等式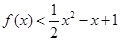 的解集为( )
的解集为( )
A.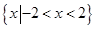 | B.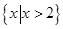 | C.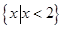 | D.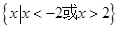 |
C
解析试题分析:令
 则原不等式为
则原不等式为 ,
,
而 ,又
,又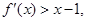 所以
所以 ,所以
,所以 在
在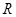 上单调递增.
上单调递增.
而 ,所以
,所以
考点:本小题主要考查抽象函数的单调性和构造函数利用函数的单调性解抽象不等式,考查了学生的构造能力和转化能力.
点评:导数主要功能之一是研究函数的单调性,所以看到题目中出现导数,自然应该能够想到要向单调性方面转化,从而成功求解.

练习册系列答案
相关题目
由曲线y=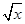 ,直线y=x-2及y轴所围成的图形的面积为
,直线y=x-2及y轴所围成的图形的面积为
A.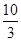 | B.4 | C.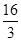 | D.6 |
设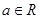 ,若函数
,若函数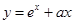 ,
,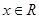 ,有大于零的极值点,则( )
,有大于零的极值点,则( )
A. | B.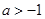 | C.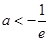 | D.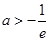 |
设定义在R上的函数 是最小正周期为
是最小正周期为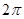 的偶函数,
的偶函数,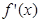 是
是 的导函数,当
的导函数,当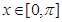 时,
时,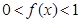 ;当
;当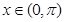 且
且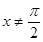 时,
时,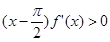 ,则函数
,则函数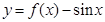 在
在 上的零点个数为
上的零点个数为
| A.2 | B.4 | C.5 | D.8 |
 等于
等于
| A.-2ln2 | B.2ln2 | C.-ln2 | D.ln2 |
函数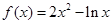 在其定义域的一个子区间
在其定义域的一个子区间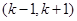 内部是单调函数,则实数
内部是单调函数,则实数 的取值范围是 ( )
的取值范围是 ( )
A.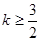 | B.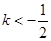 |
C.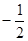 < <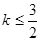 | D.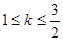 |
已知函数 且
且 ,则
,则 ( )
( )
A. | B. | C. | D. |
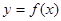 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当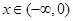 时
时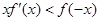 成立(其中
成立(其中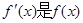 的导函数),若
的导函数),若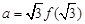 ,
,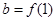 ,
,
 的大小关系是( )
的大小关系是( )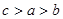
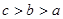
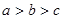
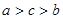
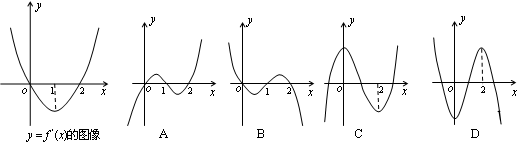
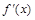 是函数
是函数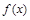 的导函数,
的导函数,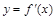 的图象如图所示,则
的图象如图所示,则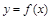 的图象最有可能的是( ).
的图象最有可能的是( ).