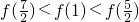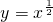题目内容
一动圆和直线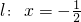 相切,并且经过点
相切,并且经过点 ,
,
(Ⅰ)求动圆的圆心θ的轨迹C的方程;
(Ⅱ)若过点P(2,0)且斜率为k的直线交曲线C于M(x1,y1),N(x2,y2)两点.
求证:OM⊥ON.
解:( I)∵动圆和直线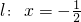 相切,并且经过点
相切,并且经过点 ,
,
∴圆心θ到 的距离等于θ到定直线
的距离等于θ到定直线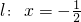 的距离,都等于圆的半径…(2分)
的距离,都等于圆的半径…(2分)
根据抛物线的定义,可得:圆心θ的轨迹C就是以F为焦点,l为准线的抛物线,…(3分)
设抛物线方程为y2=2px,其中 =
= ,解得p=1
,解得p=1
∴抛物线方程是y2=2x,即为所求轨迹C的方程.…(6分)
( II)证明:设过点P(2,0)且斜率为k的直线的方程为
y=k(x-2)(k≠0)①…(7分)
代入y2=2x消去y,可得k2x2-2(k2+1)x+4k2=0.②…(8分)
由根与系数的关系,得 .…(9分)
.…(9分)
结合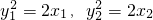 ,可得y1y2=
,可得y1y2=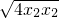 =2
=2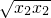 =4.…(10分)
=4.…(10分)
∴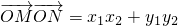 =4-4=0,
=4-4=0,
由此可得向量 夹角为90°,即OM⊥ON.…(12分)
夹角为90°,即OM⊥ON.…(12分)
分析:(I)根据圆的性质和抛物线的定义,可得动圆圆心θ的轨迹是以F为焦点,l为准线的抛物线.由此结合抛物线的标准方程加以计算,即可得到圆心θ的轨迹C的方程;
(II)设过点P(2,0)且斜率为k的直线的方程为y=k(x-2),与抛物线消去y得到关于x的一元二次方程.运用根与系数的关系算出x1x2、y1y2的值,从而得到 =0,所以
=0,所以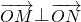 ,使结论得证.
,使结论得证.
点评:本题给出满足条件的动圆,求动圆的圆心θ的轨迹C的方程并证明OM⊥ON.着重考查了平面向量数量积的运算性质、抛物线的几何性质和轨迹方程求法等知识,属于中档题.
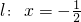 相切,并且经过点
相切,并且经过点 ,
,∴圆心θ到
 的距离等于θ到定直线
的距离等于θ到定直线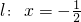 的距离,都等于圆的半径…(2分)
的距离,都等于圆的半径…(2分)根据抛物线的定义,可得:圆心θ的轨迹C就是以F为焦点,l为准线的抛物线,…(3分)
设抛物线方程为y2=2px,其中
 =
= ,解得p=1
,解得p=1∴抛物线方程是y2=2x,即为所求轨迹C的方程.…(6分)
( II)证明:设过点P(2,0)且斜率为k的直线的方程为
y=k(x-2)(k≠0)①…(7分)
代入y2=2x消去y,可得k2x2-2(k2+1)x+4k2=0.②…(8分)
由根与系数的关系,得
 .…(9分)
.…(9分)结合
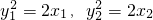 ,可得y1y2=
,可得y1y2=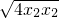 =2
=2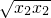 =4.…(10分)
=4.…(10分)∴
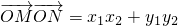 =4-4=0,
=4-4=0,由此可得向量
 夹角为90°,即OM⊥ON.…(12分)
夹角为90°,即OM⊥ON.…(12分)分析:(I)根据圆的性质和抛物线的定义,可得动圆圆心θ的轨迹是以F为焦点,l为准线的抛物线.由此结合抛物线的标准方程加以计算,即可得到圆心θ的轨迹C的方程;
(II)设过点P(2,0)且斜率为k的直线的方程为y=k(x-2),与抛物线消去y得到关于x的一元二次方程.运用根与系数的关系算出x1x2、y1y2的值,从而得到
 =0,所以
=0,所以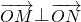 ,使结论得证.
,使结论得证.点评:本题给出满足条件的动圆,求动圆的圆心θ的轨迹C的方程并证明OM⊥ON.着重考查了平面向量数量积的运算性质、抛物线的几何性质和轨迹方程求法等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数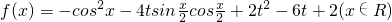
(1)当t=1时,求f(x)的最小值;
(2)若t∈R,将f(x)的最小值记为g(t),求g(t)的表达式;
(3)当-1≤t≤1时,关于t的方程g(t)=kt有且只有一个实根,求实数k的取值范围.
某地区甲校高二年级有1100人,乙校高二年级有900人,为了统计两个学校高二年级在学业水平考试中的数学学科成绩,采用分层抽样的方法在两校共抽取了200名学生的数学成绩,如下表:(已知本次测试合格线是50分,两校合格率均为100%)
甲校高二年级数学成绩:
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 10 | 25 | 35 | 30 | x |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 15 | 30 | 25 | y | 5 |
(II)若数学成绩不低于80分为优秀,低于80分为非优秀,根据以上统计数据写下面2×2列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“两个学校的数学成绩有差异?”
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
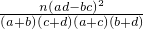 .
. 淘宝卖家在购买过某商品的所有买家中随机选择男女买家各50位进行调配,他们的评分(保留一位小数)的情况如下:
| 评价等级(分) | 0-1.0 | 1.1-2.0 | 2.1-3.0 | 3.1-4.0 | 4.1-5.0 |
| 女(人数) | 2 | 7 | 9 | 20 | 12 |
| 男(人数) | 3 | 9 | 18 | 12 | 8 |
(II)现在规定评分在3.0以下(含3.0)为不喜欢该商品,评分在3.0以上为喜欢该商品,完成表格并帮助卖家判断是否有95%以上的把握认为:买家的性别与是否喜欢该商品之间有关系.
| 喜欢该商品 | 不喜欢该商品 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
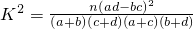 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)参考值表:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |