题目内容
设数列{an}是首项为a1（a1＞0），公差为2的等差数列，其前n项和为Sn，且
成等差数列．
（Ⅰ）求数列{an]的通项公式；
（Ⅱ）记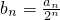
的前n项和为Tn，求Tn．
解：（Ⅰ）∵S1=a1，S2=a1+a2=2a1+2，S3=a1+a2+a3=3a1+6，
由成等差数列得，
，即
，
解得a1=1，故an=2n-1；
（Ⅱ）
，
，①
①×
得，
，②
①-②得，
=
，
∴
．
分析：（I）有数列{an}是首项为a1（a1＞0），公差为2的等差数列且成等差数列，可以先求出数列的首项即可；
（II）有 （I）和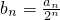，求出数列bn的通项，有通项求出前n项和为Tn．
点评：此题考查了等差数列的通项公式及等差中项，还考查了错位相减法求数列的前n项的和．
由
成等差数列得，，即，解得a1=1，故an=2n-1；
（Ⅱ）
，，①①×
得，，②①-②得，
=，∴
．分析：（I）有数列{an}是首项为a1（a1＞0），公差为2的等差数列且
成等差数列，可以先求出数列的首项即可；（II）有 （I）和
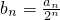，求出数列bn的通项，有通项求出前n项和为Tn．点评：此题考查了等差数列的通项公式及等差中项，还考查了错位相减法求数列的前n项的和．
练习册系列答案
相关题目
设数列{an}是首项为1公比为3的等比数列，把{an}中的每一项都减去2后，得到一个新数列{bn}，{bn}的前n项和为Sn，对任意的n∈N*，下列结论正确的是（ ）
A、bn+1=3bn，且Sn=
| ||
B、bn+1=3bn-2，且Sn=
| ||
C、bn+1=3bn+4，且Sn=
| ||
D、bn+1=3bn-4，且Sn=
|