题目内容
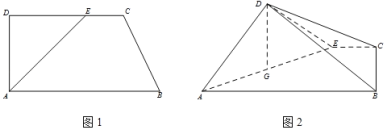
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图),![]() 为
为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求四棱锥![]() 的体积;
的体积;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(I)证明DG⊥AE,再由面面垂直的性质可得到证明;(II)分别计算DG和梯形ABCE的面积,即可得棱锥体积;(III)过点C作CF∥AE交AB于点F,过点F作FP∥AD交DB于点P,连接PC,可证平面PCF∥平面ADE,故CP∥平面ADE,根据PF∥AD计算![]() 的值.
的值.
(Ⅰ)证明:因为![]() 为
为![]() 中点,
中点,![]() ,
,
所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)在直角三角形![]() 中,易求
中,易求![]() ,则
,则![]() .
.
所以四棱锥![]() 的体积为
的体积为
![]() .
.
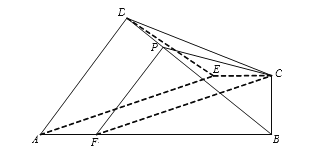
(Ⅲ) 过点C作![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() .
.
又因为![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() .
.
又因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以在![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]()

练习册系列答案
相关题目