题目内容
已知f（x）=ln（x+1）．
（1）若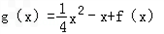
，求g（x）在[0，2]上的最大值与最小值；
（2）当x＞0时，求证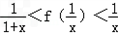
；
（3）当n∈N+且n≥2时，求证：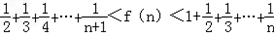
．
（1）若
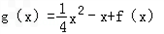，求g（x）在[0，2]上的最大值与最小值；（2）当x＞0时，求证
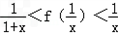；（3）当n∈N+且n≥2时，求证：
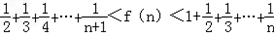．（1）解：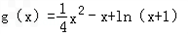
，
=
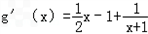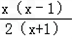
∴g（x）在[0，1]上单调减，在[1，2]上单调增
∵g（0）=0，g（1）=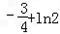
，g（2）=﹣1+ln3
∴g（x）在[0，2]上的最大值为﹣1+ln3，最小值为0
（2）证明：函数的定义域为（﹣1，+∞）
构造函数h（x）=f（x）﹣x，∴h′（x）=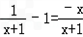
∴函数在（﹣1，0）上单调增，在（0，+∞）上单调减
∴在x=0处，函数取得极大值，也是最大值
∴h（x）≤h（0）=0
∴f（x）﹣x≤0
∵x＞0，∴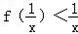
构造函数φ（x）=f（x）﹣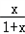
，∴φ′（x）=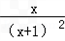 
∴函数在（﹣1，0）上单调减，在（0，+∞）上单调增
∴在x=0处，函数取得极小，也是最小值
∴φ（x）≥φ（0）=0
∴f（x）﹣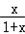
≥0
∵x＞0，∴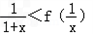
∴
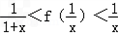
（3）证明：∵f（x）=ln（x+1），
∴f（n）﹣f（n﹣1）=f（
）
由（2）知：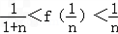
∴
∴
，
，
，…，
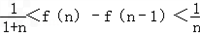
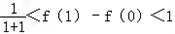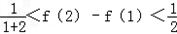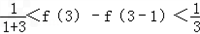叠加可得：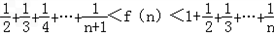
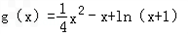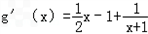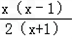
，=∴g（x）在[0，1]上单调减，在[1，2]上单调增
∵g（0）=0，g（1）=
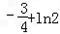，g（2）=﹣1+ln3∴g（x）在[0，2]上的最大值为﹣1+ln3，最小值为0
（2）证明：函数的定义域为（﹣1，+∞）
构造函数h（x）=f（x）﹣x，∴h′（x）=
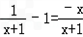
∴函数在（﹣1，0）上单调增，在（0，+∞）上单调减
∴在x=0处，函数取得极大值，也是最大值
∴h（x）≤h（0）=0
∴f（x）﹣x≤0
∵x＞0，∴
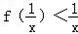
构造函数φ（x）=f（x）﹣
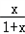，∴φ′（x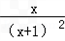）= ∴函数在（﹣1，0）上单调减，在（0，+∞）上单调增
∴在x=0处，函数取得极小，也是最小值
∴φ（x）≥φ（0）=0
∴f（x）﹣
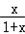≥0 ∵x＞0，∴
∴
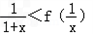
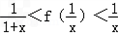
（3）证明：∵f（x）=ln（x+1），
∴f（n）﹣f（n﹣1）=f（
）由（2）知：
∴
∴
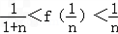
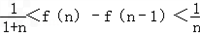
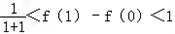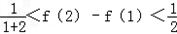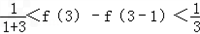，， ，…， 叠加可得：
练习册系列答案
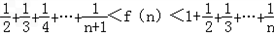
名校课堂系列答案
相关题目