题目内容
(本小题满分12分) 已知数列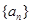 的前
的前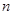 项和为
项和为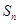 ,常数
,常数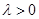 ,且
,且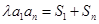 对一切正整数
对一切正整数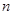 都成立。
都成立。
(Ⅰ)求数列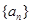 的通项公式;
的通项公式;
(Ⅱ)设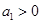 ,
,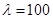 ,当
,当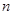 为何值时,数列
为何值时,数列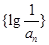 的前
的前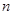 项和最大?
项和最大?
【答案】
(1)若a1 = 0, 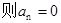 若a1
若a1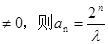 ;(2)数列{lg
;(2)数列{lg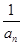 }的前6项的和最大.
}的前6项的和最大.
【解析】取n=1,得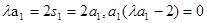
若a1=0,则s1=0,
当n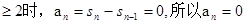
若a1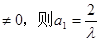 ,
当n
,
当n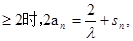

上述两个式子相减得:an=2an-1,所以数列{an}是等比数列
综上,若a1 = 0, 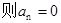
若a1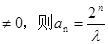 …………………………………………7分
…………………………………………7分
(2)当a1>0,且
所以,{bn}单调递减的等差数列(公差为-lg2)
则 b1>b2>b3>…>b6=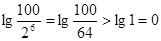
当n≥7时,bn≤b7=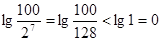
故数列{lg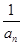 }的前6项的和最大. …………………………12分
}的前6项的和最大. …………………………12分
[点评]本小题主要从三个层面对考生进行了考查. 第一,知识层面:考查等差数列、等比数列、对数等基础知识;第二,能力层面:考查思维、运算、分析问题和解决问题的能力;第

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目