题目内容
当 的展开式的第5项的值等于
的展开式的第5项的值等于 时,x=________,此时
时,x=________,此时 =________.
=________.
2 1
分析:第一问:利用Tr+1=c6r(x )6-r(-
)6-r(- )r=c6r(-1)rx
)r=c6r(-1)rx ,令r=4,代入从而得到关于x的方程,解得x.
,令r=4,代入从而得到关于x的方程,解得x.
第二问:由题知即求首项为a1= ,公比q为
,公比q为 的等比数列前n项和的极限,由等比数列前n项和的公式sn=
的等比数列前n项和的极限,由等比数列前n项和的公式sn= (1-qn)并将第一问的x值代入再求极限可得.
(1-qn)并将第一问的x值代入再求极限可得.
解答:第一问:由Tr+1=c6r(x )6-r(-
)6-r(- )r=c6r(-1)rx
)r=c6r(-1)rx ,
,
令r=4,即T5=c64x-1= ,
,
即15x-1= ,
,
故解答为:x=2.
第二问:由x=2,
∴ (
( +
+ +…+
+…+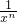 )=
)= (
( +
+ +…+
+…+ )=
)=
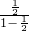 [1-(
[1-( )n]=1.
)n]=1.
故解答为;1.
点评:(1)第一问考查二项展开式特定项的问题,主要利用二项展开式第r+1项即通项公式求解.本考点是高考中的常考知识,要重视.
(2)这一问主要考查等比数列前n项和的求法以及极限的运算等知识.需要注意:当公比0<q<1或者-1<q<0时, qn=0.
qn=0.
分析:第一问:利用Tr+1=c6r(x
 )6-r(-
)6-r(- )r=c6r(-1)rx
)r=c6r(-1)rx ,令r=4,代入从而得到关于x的方程,解得x.
,令r=4,代入从而得到关于x的方程,解得x.第二问:由题知即求首项为a1=
 ,公比q为
,公比q为 的等比数列前n项和的极限,由等比数列前n项和的公式sn=
的等比数列前n项和的极限,由等比数列前n项和的公式sn= (1-qn)并将第一问的x值代入再求极限可得.
(1-qn)并将第一问的x值代入再求极限可得.解答:第一问:由Tr+1=c6r(x
 )6-r(-
)6-r(- )r=c6r(-1)rx
)r=c6r(-1)rx ,
,令r=4,即T5=c64x-1=
 ,
,即15x-1=
 ,
,故解答为:x=2.
第二问:由x=2,
∴
 (
( +
+ +…+
+…+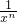 )=
)= (
( +
+ +…+
+…+ )=
)=
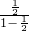 [1-(
[1-( )n]=1.
)n]=1.故解答为;1.
点评:(1)第一问考查二项展开式特定项的问题,主要利用二项展开式第r+1项即通项公式求解.本考点是高考中的常考知识,要重视.
(2)这一问主要考查等比数列前n项和的求法以及极限的运算等知识.需要注意:当公比0<q<1或者-1<q<0时,
 qn=0.
qn=0. 
练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 的展开式的第5项的值等于
的展开式的第5项的值等于 时,x= ,此时
时,x= ,此时 = .
= .