题目内容
4.在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),D(0,0,2),E(0,2,1).(Ⅰ)求证:直线BE∥平面ADO;
(Ⅱ)求直线OB和平面ABD所成的角;
(Ⅲ)在直线BE上是否存在点P,使得直线AP与直线BD垂直?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (Ⅰ)根据向量关系利用线面平行的判定定理即可证明直线BE∥平面ADO;
(Ⅱ)求出平面ABD的法向量,利用向量法即可求直线OB和平面ABD所成的角;
(Ⅲ)根据空间直线垂直的坐标关系即可得到结论.
解答 解:(I)法一:取点C(0,2,0)
则$\overrightarrow{CB}=(2,0,0),\overrightarrow{OA}=(2,0,0)$,所以$\overrightarrow{CB}=\overrightarrow{OA}$,所以OA∥CB-------------(1分)
又$\overrightarrow{OD}=(0,2,0),\overrightarrow{CE}=(0,1,0)$,所以$\overrightarrow{CE}=\frac{1}{2}\overrightarrow{OD}$,所以OD∥CE-------------(2分)
又OA∩OD=D,CE∩CB=C
所以平面OAD∥CBE-------------(3分)
所以BE∥平面ADO-------------(4分)
法二:由题意,点A,D,O所在的平面就是 xOz平面,
取其法向量为$\overrightarrow n=(0,1,0)$,-------------(1分)
而$\overrightarrow{BE}=(-2,0,1)$,所以$\overrightarrow{BE}•\overrightarrow n=0$,即$\overrightarrow{BE}⊥\overrightarrow n$,-------------(3分)
又显然点B,E不在平面ADO上,
所以BE∥平面ADO.-------------(4分)
( II)设平面ABD的法向量为$\overrightarrow m=(a,b,c)$,
因为$\overrightarrow{AB}=(0,2,0),\overrightarrow{AD}=(-2,0,2)$,
所以$\left\{\begin{array}{l}\overrightarrow{AB}•\overrightarrow m=2b=0\\ \overrightarrow{AD}•\overrightarrow m=-2a+2c=0\end{array}\right.$,所以可取$\overrightarrow m=(1,0,1)$.-------------(6分)
又$\overrightarrow{OB}=(2,2,0)$,
设OB与平面ABD所成的角为θ.
所以$sinθ=|cos<\overrightarrow{OB},\overrightarrow m>|=|\frac{{\overrightarrow{OB}•\overrightarrow m}}{{|\overrightarrow{OB}||\overrightarrow m|}}|=\frac{2}{{\sqrt{2}•2\sqrt{2}}}=\frac{1}{2}$.-------------(8分)
所以直线OB和平面ABD所成的角为$\frac{π}{6}$.-------------(9分)
(Ⅲ)假设存在点P(x,y,z),使得直线AP与直线BD垂直.
设$\overrightarrow{BP}=λ\overrightarrow{BE}$,即(x-2,y-2,z)=(-2λ,0,λ).-------------(10分)
所以$\left\{\begin{array}{l}x=2-2λ\\ y=2\\ z=λ\end{array}\right.$,
所以$\overrightarrow{AP}=(-2λ,2,λ)$.
又$\overrightarrow{BD}=(-2,-2,2)$,
所以$\overrightarrow{AP}•\overrightarrow{BD}=4λ-4+2λ=0$,-------------(11分)
解得$λ=\frac{2}{3}$,所以在直线BE上存在点P,使得直线AP与直线BD垂直,
点P的坐标为$(\frac{2}{3},2,\frac{2}{3})$.-------------(12分)
点评 本题主要考查空间直线和平面平行的判断,以及空间直线和平面所成角的求解以及空间直线垂直的判断,利用坐标法是解决本题的关键.

| A. | 360 | B. | 180 | C. | 90 | D. | 45 |
| A. | x2-8y2=1 | B. | 2x2-4y2=1 | C. | 8y2-x2=1 | D. | 4x2-2y2=1 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F(1,0),是椭圆C的右焦点,若不经过原点O的直线l:y=kx+m(k>0)与椭圆C相交于不同的两点A、B,记直线OA,OB的斜率分别为k1,k2,且k1•k2=k2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F(1,0),是椭圆C的右焦点,若不经过原点O的直线l:y=kx+m(k>0)与椭圆C相交于不同的两点A、B,记直线OA,OB的斜率分别为k1,k2,且k1•k2=k2.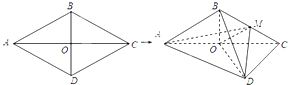 如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:
如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证: