题目内容
设a为函数 的最大值,则二项式
的最大值,则二项式 的展开式中含x2项的系数是( )
的展开式中含x2项的系数是( )A.192
B.182
C.-192
D.-182
【答案】分析:首先根据两角和的正弦公式,可得a=2,进而可得二项展开式的通项公式,令3-r=2,得r=1,将r=1代入二项展开式可得答案.
解答:解:因为 ,由题设a=2,
,由题设a=2,
则二项展开式的通项公式为 .
.
令3-r=2,得r=1,
所以含x2项的系数是(-1)×C61•25=-192,
故选C.
点评:本题考查二项式定理的应用,涉及两角和与差的公式,难度不大.
解答:解:因为
 ,由题设a=2,
,由题设a=2,则二项展开式的通项公式为
 .
.令3-r=2,得r=1,
所以含x2项的系数是(-1)×C61•25=-192,
故选C.
点评:本题考查二项式定理的应用,涉及两角和与差的公式,难度不大.

练习册系列答案
相关题目
 的最大值,则二项式
的最大值,则二项式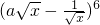 的展开式中含x2项的系数是
的展开式中含x2项的系数是 的最大值,则二项式
的最大值,则二项式 的展开式中含x2项的系数是( )
的展开式中含x2项的系数是( ) 的最大值,则二项式
的最大值,则二项式 的展开式中含x2项的系数是( )
的展开式中含x2项的系数是( ) 的最大值,则二项式
的最大值,则二项式 的展开式中含x2项的系数是( )
的展开式中含x2项的系数是( )