题目内容
设a>0,在C内解方程z2+2|z|=a.
思路分析:解复数方程时,不能简单的利用韦达定理来解,要分析清属于哪一种情况,分类求解.
解:∵a,|z|∈R,∴z2=a-2|z|∈R.∴z为实数或纯虚数.
(1)当z∈R时,原方程转化为|z|2+2|z|-a=0,解之,得z=±(-1+![]() ).
).
(2)若z为纯虚数,则z=bi(b≠0,b∈R),于是方程转化为|b|2-2|b|+a=0.
①当a=0时,解得b=±2;
②当0<a≤1时,解得b=±(1±![]() );
);
③当a>1时,方程无解.
综上,a=0时,z=±2i,z=0;
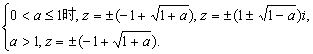

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目