Question

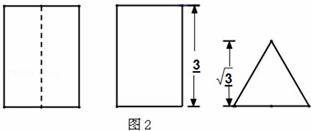
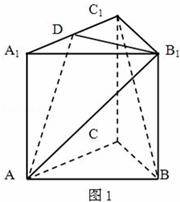
已知某几何体的直观图（图1）与它的三视图（图2），其中俯视图为正三角形，其它两个视图是矩形．已知D是这个几何体的棱A₁C₁上的中点．

（Ⅰ）求出该几何体的体积；

（Ⅱ）求证：直线BC₁∥平面AB₁D；

（Ⅲ）求证：平面AB₁D⊥平面AA₁D．

Answer 1

考点：

平面与平面垂直的判定；由三视图求面积、体积；直线与平面平行的判定．

专题：

计算题；证明题；综合题．

分析：

（Ⅰ）由三视图直接求出底面面积和高，然后求出该几何体的体积；

（Ⅱ）连接A₁B，且A₁B∩AB₁=O，要证直线BC₁∥平面AB₁D，只需证明直线BC₁平行平面AB₁D内的直线DO即可；

（Ⅲ）要证平面AB₁D⊥平面AA₁D，只需证明平面AB₁D内的直线B₁D垂直平面AA₁D即可．

解答：

解：由三视图可知该几何体为正三棱柱，底面是高为的正三角形，三棱柱的高h=3，

（Ⅰ）底面是高为的正三角形，易知底面边长为2，所以底面面积，

所求体积．

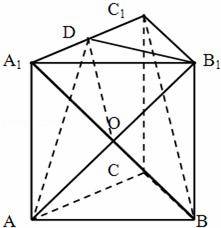
（Ⅱ）连接A₁B，且A₁B∩AB₁=O，∵正三棱柱侧面是矩形，

∴点O是棱A₁B的中点（6分）

因为D为棱A₁C₁的中点．连接DO，∴DO是△A₁BC₁的中位线，∴BC₁∥DO，又DO⊂平面AB₁D，BC₁⊄平面AB₁D，∴BC₁∥平面AB₁D．（9分）

（Ⅲ）在正三棱柱ABC﹣A₁B₁C₁中，三角形A₁B₁C₁为正三角形，∴B₁D⊥A₁C₁．，

又由正三棱柱性质知平面A₁B₁C₁⊥平面ACC₁A₁，且平面A₁B₁C₁∩平面ACC₁A₁=A₁C₁，

B₁D⊂平面A₁B₁C₁，∴B₁D⊥平面AA₁D，（12分）又B₁D⊂平面AB₁D，

∴平面AB₁D⊥平面AA₁D．（14分）

点评：

本题考查平面与平面垂直的判定，直线与平面的平行的判定，棱柱的体积，考查逻辑思维能力，空间想象能力，是中档题．