题目内容
设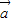 、
、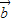 、
、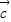 是任意的非零向量,且相互不共线,给定下列结论
是任意的非零向量,且相互不共线,给定下列结论①•
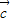 -•
-•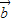 =
=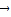
②|
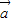 |-|
|-|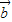 |<|
|<|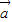 -
-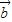 |
|③•
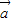 -•
-•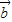 不与
不与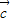 垂直
垂直④(3
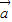 +2
+2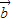 )•(3
)•(3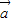 -2
-2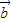 )=9
)=9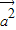 -4
-4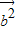
其中正确的叙述有 .
【答案】分析:①利用向量共线以及数量积的公式进行判断.②利用向量的模长关系判断.③利用向量垂直与数量积的关系判断.④利用平面向量的数量积公式进行运算.
解答:解:①因为 ,
, ,因为
,因为 、
、 、
、 是任意的非零向量,且相互不共线,所以(
是任意的非零向量,且相互不共线,所以( •
• )•
)• -(
-( •
• )•
)•
 ,所以①错误.
,所以①错误.
②由向量的减法法则知,两向量差的模一定小两向量模的差,所以②正确.
③因为 ,所以
,所以 ,所以③错误.
,所以③错误.
④因为 ,所以④正确.
,所以④正确.
故答案为:②④.
点评:本题主要考查平面向量数量积的应用,要求熟练掌握数量积的定义以及基本应用.
解答:解:①因为
 ,
, ,因为
,因为 、
、 、
、 是任意的非零向量,且相互不共线,所以(
是任意的非零向量,且相互不共线,所以( •
• )•
)• -(
-( •
• )•
)•
 ,所以①错误.
,所以①错误.②由向量的减法法则知,两向量差的模一定小两向量模的差,所以②正确.
③因为
 ,所以
,所以 ,所以③错误.
,所以③错误.④因为
 ,所以④正确.
,所以④正确.故答案为:②④.
点评:本题主要考查平面向量数量积的应用,要求熟练掌握数量积的定义以及基本应用.

练习册系列答案
相关题目
 ,
, ,
, 是任意的非零向量,且互不共线,下列命题是真命题的有
是任意的非零向量,且互不共线,下列命题是真命题的有 ;②
;② ;③
;③ 不与
不与 垂直;④
垂直;④
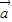 ,
,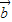 ,
,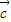 是任意的非零向量,且相互不共线,下列命题:
是任意的非零向量,且相互不共线,下列命题: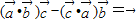 ,
,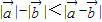 ,
,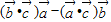 不与
不与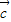 垂直,
垂直,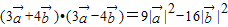 .
.