题目内容
已知数列{an}前n项和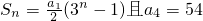 ,则an=
,则an=
- A.
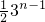
- B.3n-1
- C.3•2n-1
- D.2•3n-1
D
分析:由已知的等式,再写一式,两式相减得第n项和与第n-1项和的差为an,从而得到此数列通项公式,把n=4代入通项公式,由a4=54,得到a1,然后写出通项公式即可.
解答:∵ ①,
①,
∴n≥2时, ②,
②,
①-②得:an= ,
,
把n=4,代入,得: =54,∴a1=2,
=54,∴a1=2,
∴an=1×(3n-3n-1)=2•3n-1
故选D.
点评:本题考查数列的递推式,考查确定数列的通项,属于基础题.
分析:由已知的等式,再写一式,两式相减得第n项和与第n-1项和的差为an,从而得到此数列通项公式,把n=4代入通项公式,由a4=54,得到a1,然后写出通项公式即可.
解答:∵
 ①,
①,∴n≥2时,
 ②,
②,①-②得:an=
 ,
,把n=4,代入,得:
 =54,∴a1=2,
=54,∴a1=2,∴an=1×(3n-3n-1)=2•3n-1
故选D.
点评:本题考查数列的递推式,考查确定数列的通项,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目