题目内容
已知函数f(x)=(2x-a)2+(2-x+a)2,x∈[-1,1].(1)求f(x)的最小值(用a表示);
(2)记g(x)=f(x)-2a2,如果函数g(x)有零点,求实数a的取值范围.
【答案】分析:(1)先把函数f(x)化简为f(x)=(2x-2-x)2-2a(2x-2-x)+2a2+2的形式,令t=2x-2-x,则f(x)可看作关于t的二次函数,根据x的范围求出t的范围,再利用二次函数求最值的方法求出f(x)的最小值.
(2)关于x的方程f(x)=2a2有解,即方程t2-2at+2=0在[- ,
, ]上有解,而t≠0把t与a分离,利用函数的单调性求范围即可.
]上有解,而t≠0把t与a分离,利用函数的单调性求范围即可.
解答:解:(1)f(x)=(2x-a)2+(2-x+a)2=22x+2-2x-2a(2x-2-x)+2a2=(2x-2-x)2-2a(2x-2-x)+2a2+2
令t=2x-2-x,则当x∈[-1,1]时,t关于x的函数是单调递增
∴t∈[- ,
, ],此时f(x)=t2-2at+2a2+2=(t-a)2+a2+2
],此时f(x)=t2-2at+2a2+2=(t-a)2+a2+2
当a< -时,f(x)min=f(-
-时,f(x)min=f(- )=2a2+3a+
)=2a2+3a+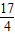
当- ≤a≤
≤a≤ 时,f(x)min=a2+2
时,f(x)min=a2+2
当a> 时,f(x)min=f(
时,f(x)min=f( )=2a2-3a+
)=2a2-3a+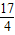 .
.
(2)函数g(x)有零点,则方程f(x)=2a2有解,即方程t2-2at+2=0在[- ,
, ]上有解,而t≠0
]上有解,而t≠0
∴2a=t+ ,
,
令y=t+ ,则y′=1-
,则y′=1-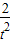 ,∴函数在(0,
,∴函数在(0,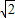 )上单调递减,(
)上单调递减,(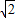 ,
, )上单调递增
)上单调递增
∴t+ ≥2
≥2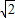
∵t+ 为奇函数,∴当t∈(-
为奇函数,∴当t∈(- ,0)时,t+
,0)时,t+ ≤-2
≤-2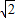
∴a的取值范围是(-∞,-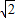 ]∪[
]∪[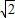 ,+∞).
,+∞).
点评:本题考查二次函数与其它函数的复合函数的最值的求法,考查函数的零点,考查学生的计算能力,属于中档题.
(2)关于x的方程f(x)=2a2有解,即方程t2-2at+2=0在[-
 ,
, ]上有解,而t≠0把t与a分离,利用函数的单调性求范围即可.
]上有解,而t≠0把t与a分离,利用函数的单调性求范围即可.解答:解:(1)f(x)=(2x-a)2+(2-x+a)2=22x+2-2x-2a(2x-2-x)+2a2=(2x-2-x)2-2a(2x-2-x)+2a2+2
令t=2x-2-x,则当x∈[-1,1]时,t关于x的函数是单调递增
∴t∈[-
 ,
, ],此时f(x)=t2-2at+2a2+2=(t-a)2+a2+2
],此时f(x)=t2-2at+2a2+2=(t-a)2+a2+2当a<
 -时,f(x)min=f(-
-时,f(x)min=f(- )=2a2+3a+
)=2a2+3a+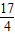
当-
 ≤a≤
≤a≤ 时,f(x)min=a2+2
时,f(x)min=a2+2当a>
 时,f(x)min=f(
时,f(x)min=f( )=2a2-3a+
)=2a2-3a+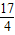 .
.(2)函数g(x)有零点,则方程f(x)=2a2有解,即方程t2-2at+2=0在[-
 ,
, ]上有解,而t≠0
]上有解,而t≠0∴2a=t+
 ,
,令y=t+
 ,则y′=1-
,则y′=1-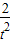 ,∴函数在(0,
,∴函数在(0,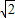 )上单调递减,(
)上单调递减,(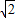 ,
, )上单调递增
)上单调递增∴t+
 ≥2
≥2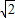
∵t+
 为奇函数,∴当t∈(-
为奇函数,∴当t∈(- ,0)时,t+
,0)时,t+ ≤-2
≤-2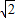
∴a的取值范围是(-∞,-
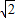 ]∪[
]∪[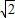 ,+∞).
,+∞).点评:本题考查二次函数与其它函数的复合函数的最值的求法,考查函数的零点,考查学生的计算能力,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|