题目内容
已知A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则A∩B=________.
{(1,2)}
分析:联立两个集合中的方程得到一个方程组,消去y得到关于x的一元一次方程,从而解得两个集合的公共元素即构成两个集合的交集.
解答:联立两个集合中的方程得 ,
,
解得:
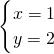 ,
,
则A∩B={(1,2)}
故答案为:{(1,2)}.
点评:此题要求学生掌握两集合的交集是由两个集合中的解析式的交点坐标构成,以及掌握解析式没有交点即两集合的交集为空集.
分析:联立两个集合中的方程得到一个方程组,消去y得到关于x的一元一次方程,从而解得两个集合的公共元素即构成两个集合的交集.
解答:联立两个集合中的方程得
 ,
,解得:
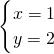 ,
,则A∩B={(1,2)}
故答案为:{(1,2)}.
点评:此题要求学生掌握两集合的交集是由两个集合中的解析式的交点坐标构成,以及掌握解析式没有交点即两集合的交集为空集.

练习册系列答案
相关题目