题目内容
四棱柱ABCD-A′B′C′D′中，AB=5，AD=3，AA′=7，∠BAD=60°，∠BAA′=∠DAA′=45°，求AC′的长．
分析：由
=
+
+
=
+
+
，利用平方法，可求出|
|，即AC′的长
| AC′ |
| AB |
| BC |
| CC′ |
| AB |
| AD |
| AA′ |
| AC′ |
解答：解：∵
=
+
+
=
+
+
∴（
）2=（
+
+
）2
=
2+
2+
2+2（
•
+
•
+
•
）
=25+9+49+2（5×3×cos60°+5×7×cos45°+3×7×cos45°）
=98+56
∴|
|=
即AC′的长为
| AC′ |
| AB |
| BC |
| CC′ |
| AB |
| AD |
| AA′ |
∴（
| AC′ |
| AB |
| AD |
| AA′ |
=
| AB |
| AD |
| AA′ |
| AB |
| AD |
| AA′ |
| AB |
| AD |
| AA′ |
=25+9+49+2（5×3×cos60°+5×7×cos45°+3×7×cos45°）
=98+56
| 2 |
∴|
| AC′ |
98+56
|
即AC′的长为
98+56
|
点评：本题以四棱柱为载体，考查向量模的求法，熟练掌握平方法求向量模的步骤是解答的关键．
练习册系列答案
相关题目
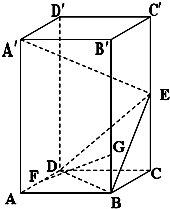已知直四棱柱ABCD-A′B′C′D′，四边形ABCD为正方形，AA′=2AB=2，E为棱CC′的中点．
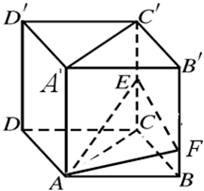已知直四棱柱ABCD-A′B′C′D′的底面是菱形，∠ABC=60°，E、F分别是棱CC′与BB′上的点，且EC=BC=2FB=2．
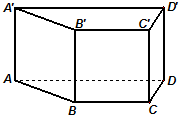在高为1的直四棱柱ABCD-A'B'C'D'中，底面ABCD是等腰梯形，AB=BC=CD=1，AD=2．