题目内容
已知数列 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,且
,且 .
.
⑴求证:数列 是等差数列;
是等差数列;
⑵设 ,求证:
,求证: ;
;
⑶设 ,
, ,求
,求 .
.
【答案】
(1)详见解析;(2)详见解析;(3)
【解析】
试题分析:(1)一般数列问题中出现数列前 的和
的和 与其项
与其项 时,则可利用关系
时,则可利用关系 找出数列的递推关系,本题可从此入手,证明数列为等差数列;(2)由(1)可求出
找出数列的递推关系,本题可从此入手,证明数列为等差数列;(2)由(1)可求出 ,根据此式的结构特征,可得
,根据此式的结构特征,可得 ,利用裂项相消法求其前
,利用裂项相消法求其前 的和
的和 后再予以判断;(3)根据数列
后再予以判断;(3)根据数列 的结构特点(等差乘等比型)可用错位相减法求和.证明数列为等差数列或等比数列,应紧扣定义,通过对所给条件变形,得到递推关系,而等差乘等比型数列的求和最常用的就是错位相减法,使用这个方法在计算上要有耐心和细心,注意各项的符号,防止出错.
的结构特点(等差乘等比型)可用错位相减法求和.证明数列为等差数列或等比数列,应紧扣定义,通过对所给条件变形,得到递推关系,而等差乘等比型数列的求和最常用的就是错位相减法,使用这个方法在计算上要有耐心和细心,注意各项的符号,防止出错.
试题解析:⑴证明: ,当
,当 时,
时, 或
或 ,又
,又 .
1分
.
1分
由 ,得
,得 ,
,


 数列
数列 是以1为首项,1为公差的等差数列;
4分
是以1为首项,1为公差的等差数列;
4分
⑵证明:由⑴知 ,
, ,
,

 .
8分
.
8分
⑶ ,
, , ①
, ①

 ②
②
由①-②得 ,
,
 .
12分
.
12分
考点:等差数列、等比数列、错位相减法.

练习册系列答案
相关题目
 的各项均为正实数,且其前
的各项均为正实数,且其前 项和
项和 满足
满足 。(1)证明:数列
。(1)证明:数列 ,求数列
,求数列 的前
的前 。
。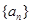 的各项均为正整数,对于
的各项均为正整数,对于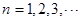 ,有
,有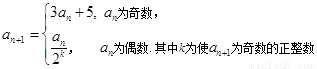 当
当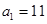 时,
时,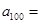 ______;
______;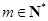 ,当
,当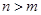 且
且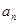 为奇数时,
为奇数时, ,则
,则
 当
当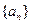 的各项均为正整数,对于
的各项均为正整数,对于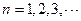 ,有
,有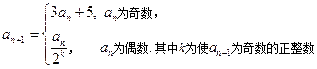 当
当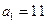 时,
时,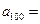 ______;
______;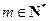 ,当
,当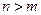 且
且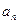 为奇数时,
为奇数时, ,则
,则