题目内容
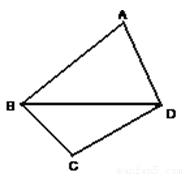
已知一颗粒子等可能地落入如右图所示的四边形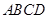 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△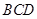 内的频率稳定在
内的频率稳定在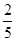 附近,那么点
附近,那么点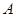 和点
和点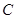 到时直线
到时直线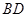 的距离之比约为( )
的距离之比约为( )
A.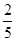 B.
B.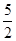 C.
C.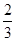 D.
D.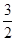
【答案】
D
【解析】
试题分析:设粒子落入△BCD内的频率为P1粒子落入△BAD内的频率为P2
点A和点C到时直线BD的距离d1,d2,根据题意:P2=1-P1=1- =
= ,然后根据
,然后根据
P1= ,P2=
,P2= ,P2:P1= d2: d1=3:2,故选D.
,P2:P1= d2: d1=3:2,故选D.
考点:本试题主要考查了几何概型中的面积类型及其应用,基本方法是:分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积,两者求比值,即为概率
点评:解决该试题的关键是先明确是几何概型中的面积类型,称设粒子落入△BCD内的频率为P1粒子落入△BAD内的频率为P2,点A和点C到时直线BD的距离d1,d2求得P2,利用其面积之比即为概率之比,再由三角形共底,求得高之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
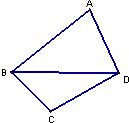 已知一颗粒子等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在
已知一颗粒子等可能地落入如图所示的四边形ABCD内的任意位置,如果通过大量的实验发现粒子落入△BCD内的频率稳定在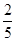 附近,那么点A和点C到直线BD的距离之比约为
附近,那么点A和点C到直线BD的距离之比约为 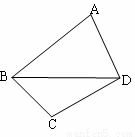
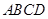 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△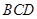 内的频率稳定在
内的频率稳定在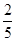 附近,那么点
附近,那么点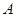 和点
和点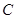 到时直线
到时直线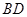 的距离之比约为
的距离之比约为 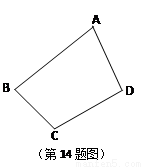
 附近,那么点A和点C到时直线BD的距离之比约为 .
附近,那么点A和点C到时直线BD的距离之比约为 .