题目内容
(2013•江西)小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以0为起点,再从A1,A2,A3,A4,A5,A6,A7,A8(如图)这8个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X.若X=0就参加学校合唱团,否则就参加学校排球队.
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.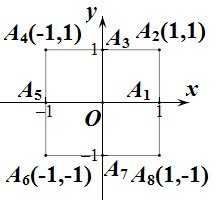
(1)求小波参加学校合唱团的概率;
(2)求X的分布列和数学期望.
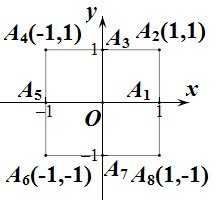
分析:(1)先求出从8个点中任意取两个点为向量的终点的不同取法,而X=0时,即两向量夹角为直角,求出结果数,代入古典概率的求解公式可求
(2)先求出两向量数量积的所有可能情形及相应的概率,即可求解分布列及期望值
(2)先求出两向量数量积的所有可能情形及相应的概率,即可求解分布列及期望值
解答:解:(1)从8个点中任意取两个点为向量的终点的不同取法有
=28种
X=0时,两向量夹角为直角共有8种情形
所以小波参加学校合唱团的概率P(X=0)=
=
(2)两向量数量积的所有可能情形有-2,-1,0,1
X=-2时有2种情形
X=1时有8种情形
X=-1时,有10种情形
X的分布列为:
EX=-2×
+(-1)×
+0×
+1×
=-
| C | 2 8 |
X=0时,两向量夹角为直角共有8种情形
所以小波参加学校合唱团的概率P(X=0)=
| 8 |
| 28 |
| 2 |
| 7 |
(2)两向量数量积的所有可能情形有-2,-1,0,1
X=-2时有2种情形
X=1时有8种情形
X=-1时,有10种情形
X的分布列为:
X |
-2 |
-1 |
0 |
1 | ||||||||
| P |
|
|
|
|
| 1 |
| 14 |
| 5 |
| 14 |
| 2 |
| 7 |
| 2 |
| 7 |
| 3 |
| 14 |
点评:本题主要考查了古典概率的求解公式的应用及离散型随机变量的分布列及期望值的求解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 (2013•江西)小波已游戏方式决定是去打球、唱歌还是去下棋.游戏规则为以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记住这两个向量的数量积为X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋
(2013•江西)小波已游戏方式决定是去打球、唱歌还是去下棋.游戏规则为以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记住这两个向量的数量积为X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋