Question

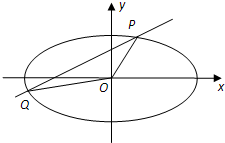已知中心在原点O，焦点在x轴上，离心率为

3

2

的椭圆过点(

2

，

2

2

)．设不过原点O的直线l与该椭圆交于P，Q两点，且直线OP，PQ，OQ的斜率依次成等比数列，求△OPQ面积的取值范围．

Answer 1

分析：根据中心在原点O，焦点在x轴上，离心率为

3

2

的椭圆过点(

2

，

2

2

)，利用待定系数法，求出几何量，可得椭圆的方程．设直线l的方程为y=kx+m（m≠0），代入椭圆方程，利用韦达定理，结合直线OP，PQ，OQ的斜率依次成等比数列，求出k的值，表示出△OPQ面积，即可求出△OPQ面积的取值范围．

解答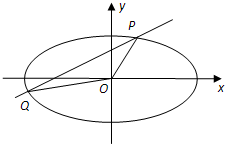：解：由题意可设椭圆方程为 

x2

a2

+

y2

b2

=1（a＞b＞0），
由 

c a = 3 2 2 a2 + 1 2b2 =1

得

a=2 b=1

，
所以，椭圆方程为

x2

4

+y2=1．                  …（4分）
由题意可知，直线l的斜率存在且不为0，
故可设直线l的方程为y=kx+m（m≠0），P（x₁，y₁），Q（x₂，y₂），则
由

y=kx+m x2+4y2-4=0

，消去y得（1+4k²）x²+8kmx+4（m²-1）=0．
△=64k²m²-16（1+4k²）（m²-1）=16（4k²-m²+1）＞0，
且x1+x2=

-8km

1+4k2

，x1x2=

4(m2-1)

1+4k2

．
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2．  …（8分）
因为直线OP，PQ，OQ的斜率依次成等比数列，
所以，

y1

x1

•

y2

x2

=

k2x1x2+km(x1+x2)+m2

x1x2

=k2，即

-8k2m2

1+4k2

+m2=0，
又m≠0，所以k2=

1

4

，即k=±

1

2

．                   …（12分）
由于直线OQ的斜率存在，且△＞0，得0＜m²＜2且m²≠1．
设d为点O到直线l的距离，则S△OPQ=

1

2

d|PQ|=

1

2

|m|

1+k2

1+k2

|x1-x2|=

1

2

|m|

(x1+x2)2-4x1x2

=

m2(2-m2)

，
所以S_△OPQ的取值范围为（0，1）．                        …（15分）

点评：本题考查椭圆的方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查三角形面积的计算，考查学生分析解决问题的能力，综合性强．