Question

直三棱柱ABC—A₁B₁C₁的底面为等腰直角三角形，∠BAC=90°，AB=AC=2，AA₁=2，E、F分别是BC、AA₁的中点.

(1)求异面直线EF和A₁B所成的角；

(2)求直三棱柱ABC—A₁B₁C₁的体积.

Answer 1

思路解析：要求异面直线所成的角，可以考虑求相关向量的夹角，而求相关向量的夹角时，可以先建立恰当的坐标系，从而得到相关的向量的坐标，利用向量的数量积知识求得结果.

解：(1)以A为坐标原点,以AB、AC、AA₁所在直线分别为x轴、y轴、z轴建立如图所示的直角坐标系，则A₁(0,0,2)、B(2,0,0)、C(0,2,0).

 

∵E、F分别是BC、AA₁的中点，

∴E(1,1,0)、F(0,0,).

∴=(-2,0,2)，=(-1,-1,).设与的夹角为θ，

则cosθ==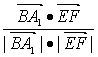

∵0≤θ≤π.∴θ=，∴异面直线EF和A₁B所成的角为.

(2)直三棱柱ABC—A₁B₁C₁的体积V=AB·AC·AA₁=×2×2×2=4.