题目内容

在正方体ABCD—A1B1C1D1中，棱长为a,M、N分别为A1B和AC上的点，A1M=AN=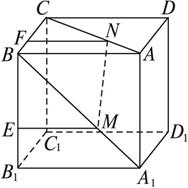a,求证:MN∥平面BB1C1C.

证明：因为正方体棱长为a,故面对角线A1B=AC=a.而A1M=AN=a,所以M、N分别是A1B和AC上的三等分点.如图,在B1B、BC上各取点E、F，使得B1E=BF=a,则

但

∴

∴,即MN∥EF.∵MN平面BB1C1C.

∴MN∥平面BB1C1C.

练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
①四边形BFD′E一定是平行四边形；
②四边形BFD′E有可能是正方形；
③四边形BFD′E在底面ABCD内的投影一定是正方形；
④平面BFD′E有可能垂直于平面BB′D．
以上结论正确的为
①③④
．（写出所有正确结论的编号）
如图，在正方体ABCD-A′B′C′D′中，E为D′C′的中点，则二面角E-AB-C的大小为
45°
45°
．
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
（1）若M为BB′的中点，证明：平面EMF∥平面ABCD．
（2）求异面直线EF与AD′所成的角．
如图在正方体ABCD-A  1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（　　）
在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交棱AA′于E，交棱CC′于F，则：
①四边形BFD′E一定是平行四边形；
②四边形BFD′E有可能是正方形；
③四边形BFD′E有可能是菱形；
④四边形BFD′E有可能垂直于平面BB′D．
其中所有正确结论的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网