题目内容
已知二次函数f (x)=x2+mx+n对任意x∈R,都有f (-x)=f (2+x)成立,设向量 =( sinx,2 ),
=( sinx,2 ), =(2sinx,
=(2sinx, ),
), =( cos2x,1 ),
=( cos2x,1 ), =(1,2),
=(1,2),
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)当x∈[0,π]时,求不等式f ( •
• )>f (
)>f ( •
• )的解集.
)的解集.
解:(Ⅰ)设f(x)图象上的两点为A(-x,y1)、B(2+x,y2),
因为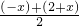 =1
=1
f (-x)=f (2+x),所以y1=y2
由x的任意性得f(x)的图象关于直线x=1对称,
∴x≥1时,f(x)是增函数;x≤1时,f(x)是减函数.
(Ⅱ)∵ •
• =(sinx,2)•(2sinx,
=(sinx,2)•(2sinx, )=2sin2x+1≥1,
)=2sin2x+1≥1,
 •
• =(cos2x,1)•(1,2)=cos2x+2≥1,
=(cos2x,1)•(1,2)=cos2x+2≥1,
∵f(x)在是[1,+∞)上为增函数,
∴f ( •
• )>f (
)>f ( •
• )?f(2sin2x+1)>f(cos2x+2)
)?f(2sin2x+1)>f(cos2x+2)
?2sin2x+1>cos2x+2?1-cos2x+1>cos2x+2
?cos2x<0?2kπ+ <2x<2kπ+
<2x<2kπ+ ,k∈z
,k∈z
?kπ+ <x<kπ+
<x<kπ+ ,k∈z
,k∈z
∵0≤x≤π,∴ <x<
<x<
综上所述,不等式f ( •
• )>f (
)>f ( •
• )的解集是:{ x|
)的解集是:{ x| <x<
<x< }.
}.
分析:(Ⅰ)由条件f (-x)=f (2+x)可知f(x)的图象关于直线x=1对称,又由于函数图象开口向上,故可求函数f (x)的单调区间;
(Ⅱ)利用函数的单调性将函数符号脱去,从而转化为解三角不等式.
点评:本题主要考查函数的对称性,利用函数的单调性,求解三角不等式,有一定的综合性.
因为
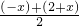 =1
=1f (-x)=f (2+x),所以y1=y2
由x的任意性得f(x)的图象关于直线x=1对称,
∴x≥1时,f(x)是增函数;x≤1时,f(x)是减函数.
(Ⅱ)∵
 •
• =(sinx,2)•(2sinx,
=(sinx,2)•(2sinx, )=2sin2x+1≥1,
)=2sin2x+1≥1, •
• =(cos2x,1)•(1,2)=cos2x+2≥1,
=(cos2x,1)•(1,2)=cos2x+2≥1,∵f(x)在是[1,+∞)上为增函数,
∴f (
 •
• )>f (
)>f ( •
• )?f(2sin2x+1)>f(cos2x+2)
)?f(2sin2x+1)>f(cos2x+2)?2sin2x+1>cos2x+2?1-cos2x+1>cos2x+2
?cos2x<0?2kπ+
 <2x<2kπ+
<2x<2kπ+ ,k∈z
,k∈z?kπ+
 <x<kπ+
<x<kπ+ ,k∈z
,k∈z∵0≤x≤π,∴
 <x<
<x<
综上所述,不等式f (
 •
• )>f (
)>f ( •
• )的解集是:{ x|
)的解集是:{ x| <x<
<x< }.
}.分析:(Ⅰ)由条件f (-x)=f (2+x)可知f(x)的图象关于直线x=1对称,又由于函数图象开口向上,故可求函数f (x)的单调区间;
(Ⅱ)利用函数的单调性将函数符号脱去,从而转化为解三角不等式.
点评:本题主要考查函数的对称性,利用函数的单调性,求解三角不等式,有一定的综合性.

练习册系列答案
相关题目